本文最后更新于：2023年12月7日下午

论文笔记 Exploring Temporal Concurrency for Video-Language Representation Learning

论文链接：ICCV 2023 Open Access Repository (thecvf.com)

代码链接（暂为空库）：https://github.com/hengRUC/TCP

人大高瓴人工智能学院+京东的一篇ICCV23，23.9月发布，与同团队的一篇CVPR2023 HIghlight前作联系紧密，本文也会进行介绍。这篇文章主要提出了两个Loss，分别探索长视频模态间的时序共现性和模态内部的动态演变性，从而进行更好的多模态表征学习。

额外参考：

同团队前作（CVPR23 Highlight）：Modeling Video as Stochastic Processes for Fine-Grained Video Representation Learning

同团队数据集前作：Long-Form Video-Language Pre-Training with Multimodal Temporal Contrastive Learning

借鉴的NLP领域原作（ICLR22 Oral）：Language Modeling via Stochastic Processes

借鉴的李飞飞原作（CVPR19）：D³TW: Discriminative Differentiable Dynamic Time Warping for Weakly Supervised Action Alignment and Segmentation

研究思路

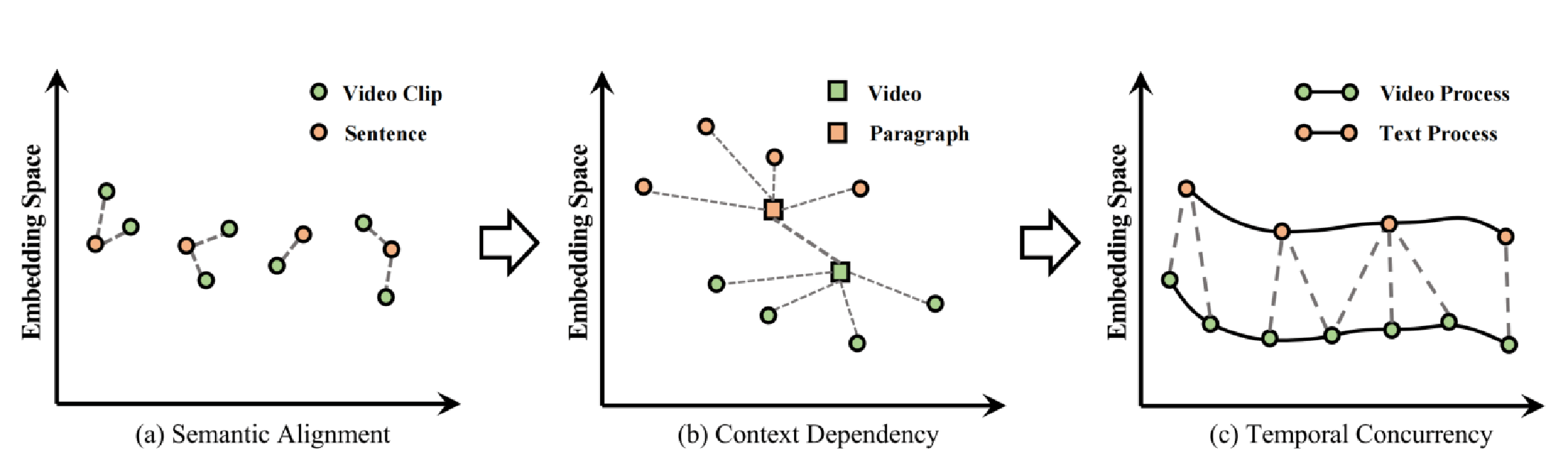
如上图所示，目前的Video-Language模型一部分像(a)那样，进行离散的跨模态对齐，处理短视频【类似CLIP、HERO、Frozen】。它们没有充分利用时序信息（短视频时序性不强）。另一部分像(b)那样，利用了长视频的时序信息，但是添加了额外的时序模块来获得全局表征，然后进行跨模态对齐【HD-VILA、MERLOT】。它们虽然考虑到了时序信息，但是没有考虑到两个模态序列的一致性或共现性（concurrency）。

这篇文章认为VL学习需要考虑模态内的时序信息以及模态间的时序对齐，提出了Temporal Concurrent Processes（TCP）的方法，即将两个模态建模为一种具有时序相似性的过程。视频在播放的时候显然是有时序性的，视频的进行是有一种内在的逻辑的，比如一个炒鸡蛋的教程视频，会先打碎鸡蛋，然后再将鸡蛋放到锅里炒，最后盛出。同样，视频对应的语言也有时序性，比如教程视频中，旁白一步步的介绍步骤。而且，两个模态的时序性还是相互关联的，其演变顺序是相同的，不可能视频是打碎鸡蛋->炒鸡蛋->盛出鸡蛋，而文本是打碎鸡蛋<-炒鸡蛋<-盛出鸡蛋。

这篇文章对于模态间和模态内分别提出了基于soft-dynamic time warping（soft-DTW）的损失函数和Process-wised Regularization Term（PRT）损失函数。其中，PRT是其前作CVPR23 Highlight提出的Modeling Videos as Stochastic Process（VSP），其思路如下：

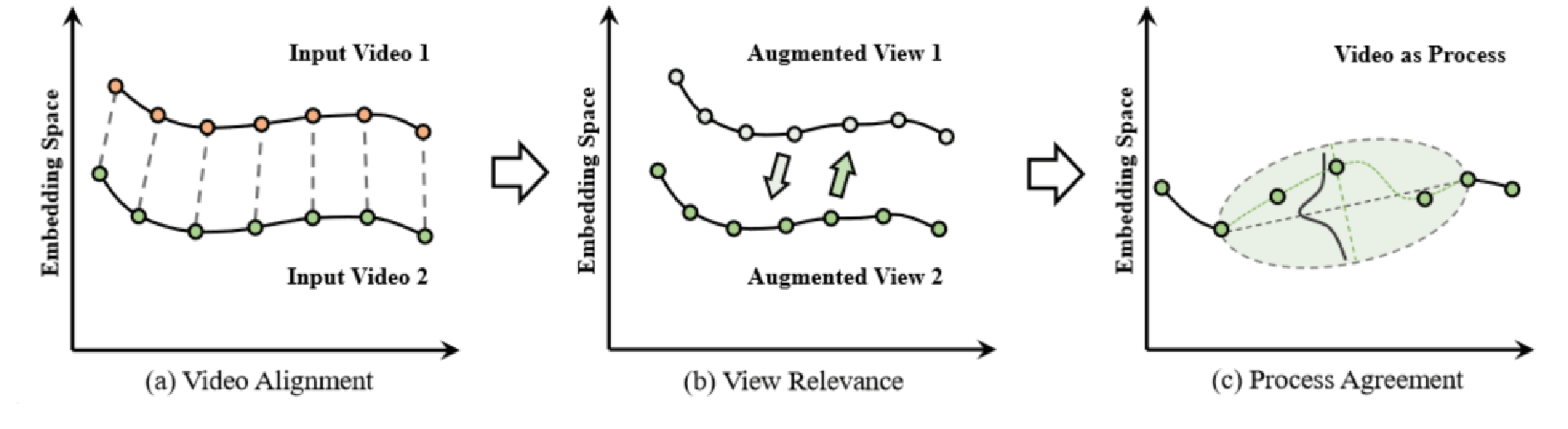
对于细粒度的视频表征学习来说，有的进行Video Alignment任务的方法如(a)所示，对于两个视频的相同时间的特征进行匹配，需要特定的数据集（比如同一个动作，有多个视角的视频）；有的如(b)所示，对于同一个视频的不同数据增强view进行对齐（图像上如SimCLR、MoCo）。这篇文章认为其他方法忽视了视频内在的动态过程特点，所以本文将视频建模为一种随机过程（如©所示），具体来说是布朗桥过程（Brownian bridge），并使用基于过程的对比学习损失来进行表征学习。

方法

基础框架

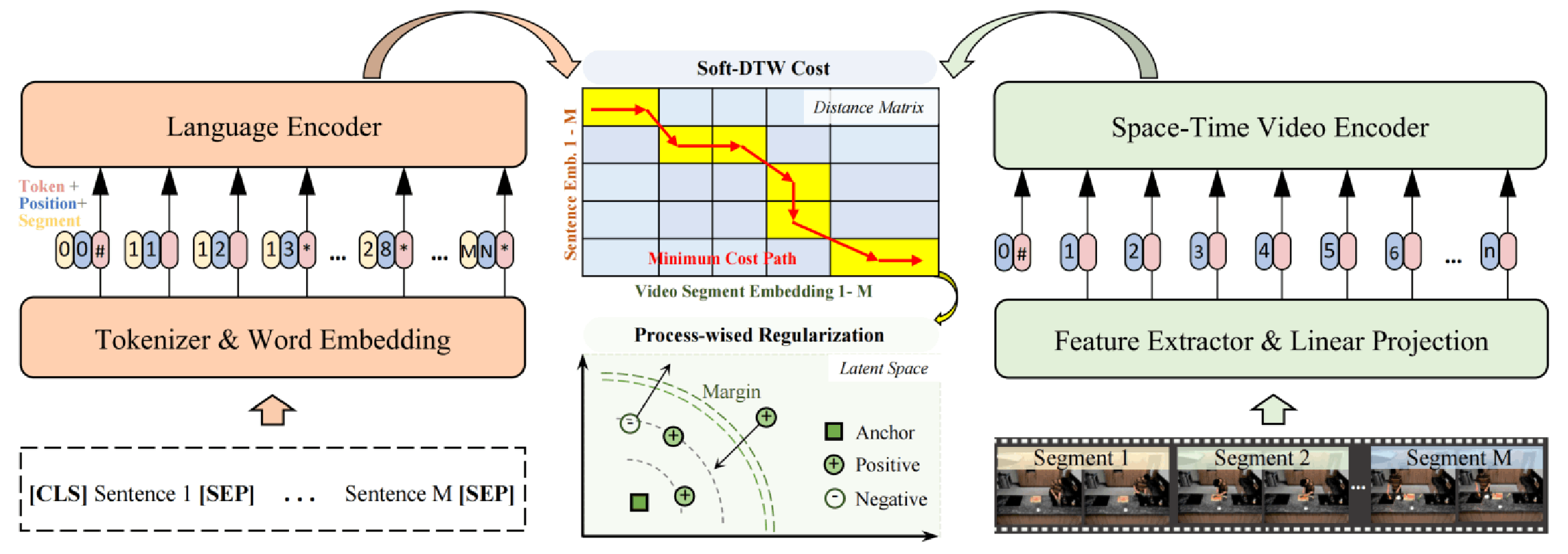
如图所示是这篇文章的基础框架，Language Encoder是BERT-base，Video Encoder是Swin Transformer（IN21K预训练）+AvgPooling，输入数据是平均120s的长视频和对应的有多个句子的段落文本。

在论文叙述中，应该是video包含segment，而segment包含clip，一个clip包含多帧，多帧的swin特征通过avgpool得到C维的clip级特征；文本则是Paragraph包括多个sentence，每个sentence都有对应的一个特征。但是实际上，貌似直接用的是segment的特征，没说怎么通过clip级别特征得到的。

锐评这个框架的话，其实对时序没做什么特殊的处理，感觉是一个比较弱的baseline。

Soft-DTW

DTW算法最早用来识别两段语音是否为同一个单词，如下图所示，上下两条波形非常相似，但是假如使用欧几里得距离来计算，由于没有对齐，结果相似度并不会很高，而假如使用DTW算法，使一个点能对应另一段语音里的多个点，那么就会使波形对齐，从而使相似度的计算更加合理。

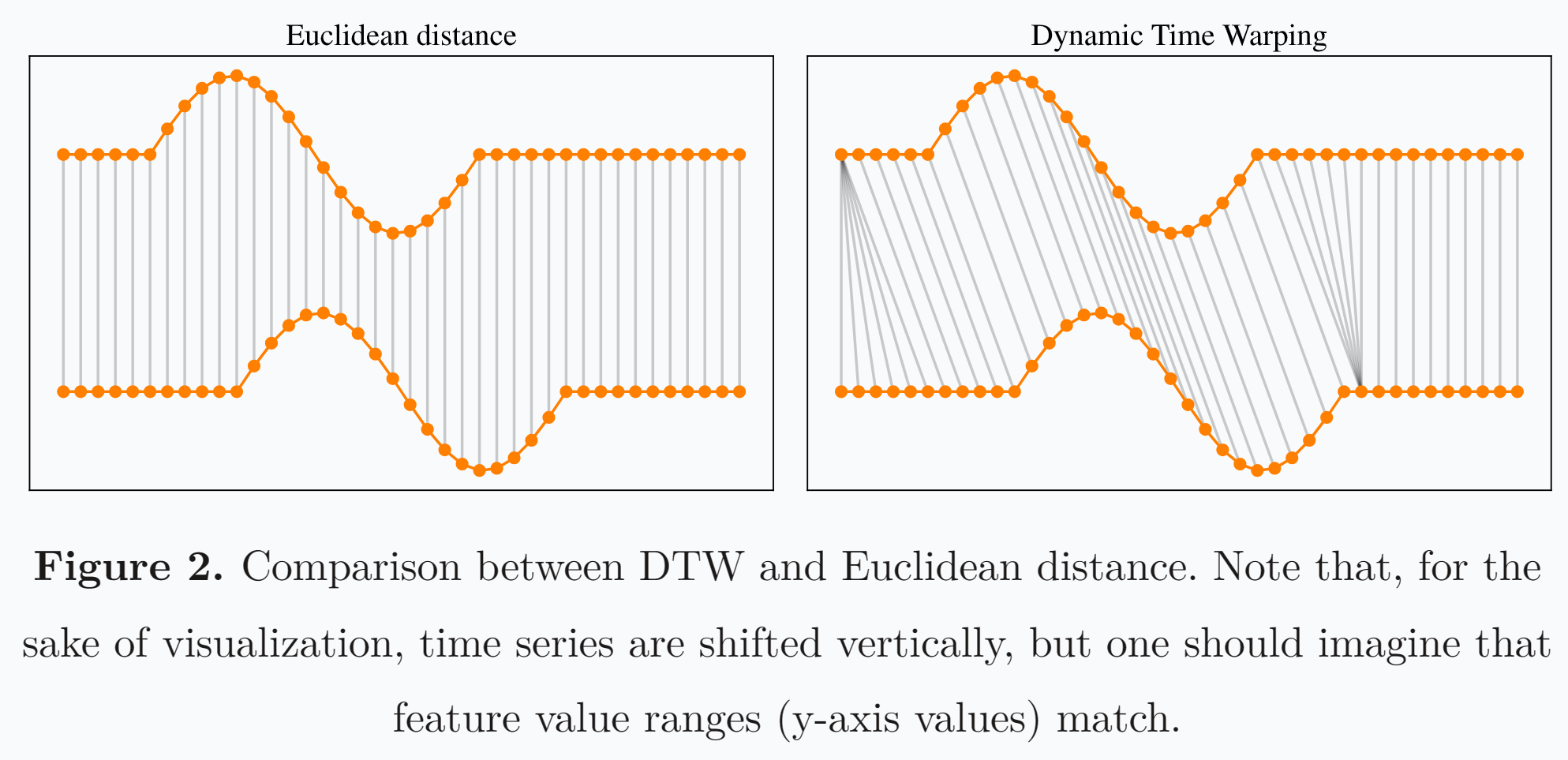
之后，李飞飞将DTW拓展到了深度学习视频领域（D³TW: Discriminative Differentiable Dynamic Time Warping for Weakly Supervised Action Alignment and Segmentation），进行Weakly Supervised Action Alignment任务。

D3TW

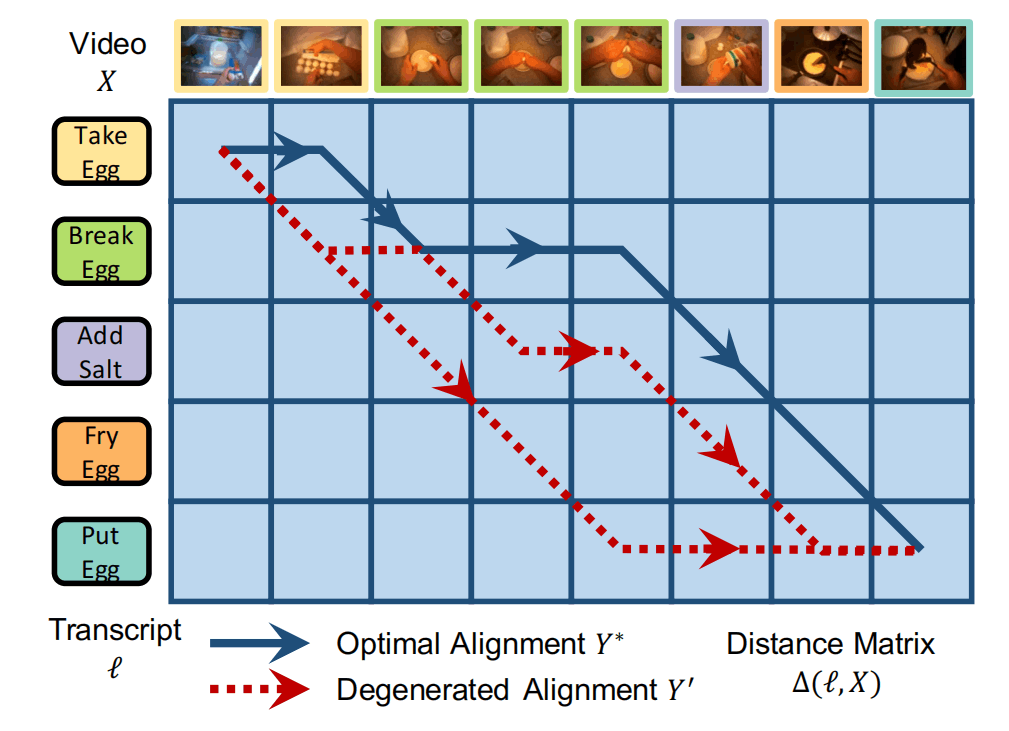
Weakly Supervised Action Alignment就是给你一个长视频，还有按照顺序排布的过程标签，需要模型求出每个标签对应的视频时间段，并且符合时间段并集是整个视频、没有交集的条件。这种情况的两个序列长度不同，并且提取出的特征可以计算相似度，所以应用DTW算法如下：

首先确定一个距离矩阵（不需要全部计算），表示标签与帧的距离，并令第一个标签与第一帧对齐。
之后根据更近的距离，选择↘️或➡️方向走，直到走到最右下角，就确定好了一条路径。

如图蓝色路径就是最终确定的路径，通过这个方法，就能从粗粒度的两个序列中获得更细粒度的自监督信号。然而，在深度学习中，“选择更近的距离”蕴含了min操作，而min是不可微分的，所以李飞飞论文使用了soft-minimum操作，如下所示，使用这个公式，在 $\lambda \rightarrow 0$ 的时候，结果就会接近于序列最小值，而且这个操作有利于梯度的传递。

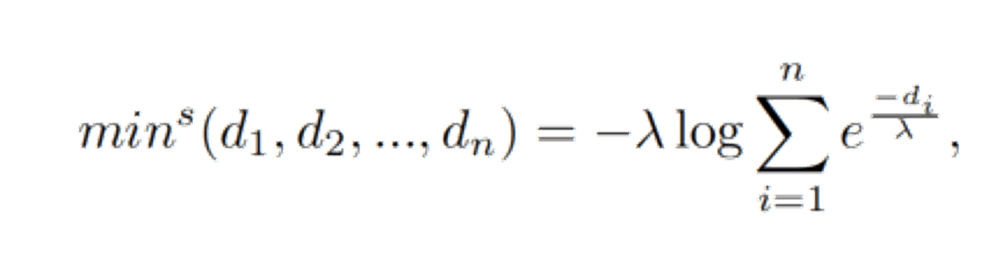
soft-minimum

具体的推导可见下面这个pdf：https://www.johndcook.com/soft_maximum.pdf

接下来，介绍这篇文章是如何使用这种soft-DTW的。

soft-DTW

这篇文章使用的soft-DTW算法使用了递归的公式，注意这里小d是距离矩阵，表示某个segment特征与sentence特征的欧几里得距离，可以直接求出来，大D是代价矩阵，表示走最佳路径到此处的代价。与李飞飞不同的是，这里可以视作往⬇️或↘️或➡️方向走。

讨论：

本质上来说，Soft-DTW是一种利用粗粒度标签实现的细粒度的对比损失。

Soft-DTW在路径上的相似度点为正例，而被soft-minimum淘汰的点为负例，负例的选择仅在instance的内部。而InfoNCE的负例就在一个batch的多个instance中选择。目前学术界的普遍结论是，在对比学习的时候应该引入尽量多或者尽量好的负样本。SimCLR暴力地把InfoNCE的batch size提升到了4096，Memory Bank的方法则通过引入不训练的负样本库来减少开销，Kaiming的MoCO进一步通过动量编码器，把负样本的数量更是提升到了65535。负样本能够保证数据不会坍缩到一个点，是非常重要的。但是本文在instance内选择负样本，是否能够选择到hard-negative的负样本是有疑问的。

除此以外，Soft-DTW可以放松对标签的需求，InfoNCE在这种情况下只能计算video-paragraph的对比损失，要实现更细粒度，就需要更细的标签（segment-sentence）。然而，在目前的训练数据中，一个segment是通过ASR来得到对应的sentence的，也就是说实际上是有更细粒度的标签的，所以这种“放松”的意义可能在其他情况下更能体现。

实际上，如上图所示，在没有给出对角线为正例的信号下，Soft-DTW引导的学习仍然学到了“对角线大，两头小”的相似矩阵。

PRT

PRT将视频建模为布朗桥随机过程，通过起始点和终点估计中间值的分布，并让中间值趋近于这个分布。下面从布朗运动开始解释：

布朗运动指的是一个粒子开始在原点，每一时刻，粒子随机移动一个步长，步长的值由正态分布决定。这个随机过程B(t)的期望为0，方差为t（与时间成正比，如上图所示）。

图来自https://demonstrations.wolfram.com/BrownianBridge/

布朗桥则是已知起点和终点的布朗运动，其概率分布是在给定 $B(a)=A$ 和 $B(b)=B$ 的情况下的布朗运动的条件概率。其统计特性如下所示。其实比较好理解，对于均值来说，就是起点与终点根据时间不同的一个线性插值，距离起点更近那起点的权重就高一些，反之亦然（下面公式 $t-t_1/t_2-t_1$ 就是距离起点的长度比例， $b-a$ 就是起点与终点的均值的变化值）。对于方差来说，就是对于 $t$ 的一个一元二次函数，可以发现 $t=t_1,t_2$ 是零点，就是说对于确定的点，方差肯定就是0了，而在中点，是不确定性最高的地方。

回到视频上来，论文假设视频在特征空间，从开始帧平滑地演化到结束帧，如下图所示，那么这个视频就能看作是一个布朗桥，已知起点（开始帧）和终点（结束帧），中间的帧应该符合高速分布，并且高斯分布的均值依据布朗桥定义如下：

公式很容易理解，其中A和T表示开始和结束，t是A与T中间的一点，如下图所示，t距离边界的比例定义为 $\alpha$ 和 $1-\alpha$ ，然后均值就是根据比例的A、T特征的插值。方差是下图右边绿色的这个函数，也比较好理解。

现在得到的这个 $p$ 是我们对 $t$ 点的分布的估计，而z实际的特征是 $z_t$ ，那么论文就定义了实际特征距离估计分布的距离 $d(z_A,z_t,z_T)$ ：

公式很简单，分子是 $z_t$ 与估计均值的欧几里得距离，分母是方差，由于加了一个负号，这里应该理解为相似度，即数值越高越相似。

公式没有解释是怎么得到的，这里给出一个基于KL散度的推导猜测：

也就是把 $z_t$ 看作是一个均值为 $z_t$ ，方差与目标相同的分布，然后计算 $z_t$ 去趋近布朗桥 $t$ 时刻的信息损失（KL散度）。注意这里的假设！

在有了相似度之后，前作论文和借鉴的NLP原作中定义的损失函数如下：

以在该随机过程的 $z_t$ 为正例，在batch内其它随机过程的 $z_t$ 为负例。

而在ICCV的这篇论文中，定义的损失函数有一点不一样：

就是采用了Triplet Margin的loss

Triplet Margin Loss

L=max(正例距离-负例距离+margin, 0)

当负例距离-正例距离大于margin时，很理想，不优化。

当负例距离-正例距离小于margin时，虽然是对的，但是仍然需要优化。

当负例距离-正例距离<<0时，非常错误，需要优化。

ICLR论文中的图

对随机过程的假设的验证

在ICLR的语言模态论文中，附录的Fig7有下面这张图：

纵轴是隐藏变量的L1范数，横轴是时间，左边图是上下文匹配的文本，右图是上下文不匹配的文本。可以发现，对于匹配的上下文，模型可以在隐空间中探索出一条平滑变化的路径，而对于不匹配的上下文，这种特性就消失了。

在CVPR的视频模态论文中，附录有下面这张图：

选择Pouring数据集的验证集，这个数据集包括一个完整行为以及其不同phase的子动作。假设有 $N$ 个视频， $M$ 个phase，每个phase固定抽19帧，所以得到了 $(N\times M)\times 19$ 个时间点，然后 $NM$ 个数据对于同一个时间点计算距离的均值和方差。

先看方差，呈现两头小，中间大的形式，和下图我画的这个绿色的线就很像。而选择其中某一点看直方图，也发现中间大两头小大致符合正态分布的PDF。

对于均值，发现不同时间点的距离比较稳定，在6.5上下浮动，可以认为是最终学习到的特征与布朗桥接近。

但是6.5是高还是低？这个比较难解释，所以我重新思考了一下距离的公式：
$\begin{align} d&=\frac{(X-\mu)^2}{2\sigma^2}, \quad X \sim \mathcal{N}(\hat{\mu},\hat{\sigma}^2) \\ Ed &= E[\frac{1}{2\sigma^2}(X^2-2\mu X + \mu^2)] \\ &= \frac{1}{2\sigma^2} ((EX)^2+DX - 2\mu EX + \mu^2) \\ &= \frac{1}{2\sigma^2} (\hat{\mu}^2+\hat{\sigma}^2-2\mu\hat{\mu}+\mu^2) \\ &\text{当}\ X \rightarrow (\mu,\sigma^2)\\ &= \frac{1}{2} \end{align}$
啊咧🤔，怎么回事，居然在最理想的情况下，距离的期望不是0，是0.5？继续求一下方差：
$\begin{align} Dd &= D[\frac{1}{2\sigma^2}(X^2-2\mu X + \mu^2)] \\ &= \frac{1}{4\sigma^4}[DX^2-4\mu^2DX] \\ \because E(X^4) &= 3\sigma^4 + 6\sigma^2\mu^2 + \mu^4 \\ E(X^2) &= \mu^2+\sigma^2 \\ \therefore DX^2 &= E(X^4)-E(X^2)^2 = 2\sigma^4 + 4\mu^2\sigma^2 \\ \therefore Dd &= \frac{1}{4\sigma^4}[2\hat{\sigma}^4 + 4\hat{\mu}^2\hat{\sigma}^2-4\mu^2\hat{\sigma}^2] \\ &\text{当}\ X \rightarrow (\mu,\sigma^2)\\ &= \frac{1}{2} \end{align}$
啊咧🤔，好像和直觉不一样，也应该是一个定值诶。

问题在于，之前布朗桥的方差是一元二次函数，是以X为变量的，而这里是用d作为变量，所以对应的方差的含义也发生了变化。至于论文的图嘛……画错了？

论文还给出了一个可视化的结果，如下图所示是一个视频的4个子动作的embedding的t-SNE降维可视化，子动作的顺序是绿→紫→黄→蓝。可以发现在子动作内部，embedding是连续且顺滑的，在整个视频的范围内，embedding也是连续且顺滑的。(b)图就是比较简单的把两个具有相同过程的视频计算相似度，对角线更相似。