本文最后更新于:2023年2月21日 下午
计算机视觉学习笔记#4 局部特征提取 Harris角点检测、SIFT尺度不变检测(附代码)
之前我们学习了提取图像边缘、拟合图中的直线或者圆,这次就来看看局部特征点的提取。**局部特征(Local Feature)**相较于全局特征(Global Feature)来说关注的图像面积更小,只关心一小块邻域,能在保留图像重要信息的同时减少处理数据量,假如图像中物体被遮挡、视角发生改变,局部特征仍然能够被识别出来。
局部特征在图像对齐、图像拼接、动作追踪、机器人导航、图像检索、目标识别等领域中被广泛使用,其中图像对齐指的是下图这种将一张图像对齐成另一张更端正的图像;图像拼接就是类似手机上全景拍照功能,拿着手机扫一圈自动合成成一张图像;动作追踪则是识别一个物体的运动轨迹,可以用来做电子防抖。


Harris 角点检测
**Harris 角点检测(Harris Corner Detector)**是被广泛运用于计算机视觉系统中的一种代表性方法,能够检测不同方向的角点。**为什么要检测角点呢?**下图是同一个柜子的两个不同视角的照片:我们假如从左图选择边上的黄色方块区域,然后想要从B图也找到这个区域,那还是比较难的,因为边上有很多相似的点;但是我们假如从左图选择出了桌角的点,那么在右图也很轻松能找到那个角。

角点顾名思义就是图像的角附近的点,假如我们放一个小滑窗到平坦的区域,那么这个滑窗往所有方向移动的时候内容变化都不大;假如放在边上,那滑窗沿着边的方向变化小,沿着边法线的方向变化大;假如放到角点,那么这个滑窗往所有方向移动的时候内容变化都很大。利用这个性质,我们就能来检测角点。
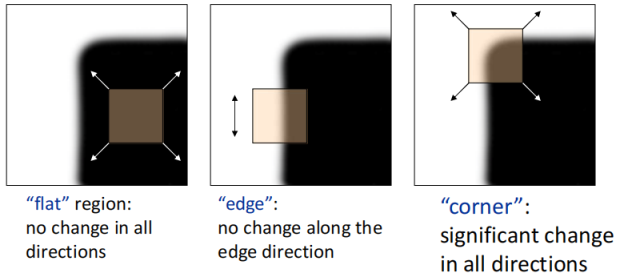
既然上边说了“内容变化”,我们先来公式化这个概念吧,滑窗可以看做是∑x,yI(x,y),施加了一个(u,v)的移动后滑窗内容就变成了∑x,yI(x+u,y+v),那么显而易见**“内容的变化”就是这两者的差,这种变化我们可以看做是能量函数(Energy)**。在实际应用中我们会取差值的平方,并额外乘一个窗函数。
E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2

然而实际中,上面这个公式在计算机上实现不是很方便,窗口每到一个地方都要往四周滑动并记录值,接下来做一些数学题可以用二元泰勒展开简化它。第一行是二元泰勒展开的定义,所以我们把能量函数近似成第二行这样,其中Ix是图像在x方向的偏导,然后第三行我们化成矩阵的形式,就可以发现计算E(u,v)只需要偏移量u,v和滑窗内部各像素的梯度了。最后,第四行我们把偏移量挪出来,发现能量函数主要与矩阵M有关。
∵f(x+u,y+v)≈f(x,y)+ufx+vfy(Taylor Expansion)∴E(u,v)=x,y∑w(x,y)(u2Ix2+2uvIxIy+v2Iy2)=[u,v]x,y∑w(x,y)[Ix2IxIyIxIyIy2][uv]=[u,v]M[uv]
这个化简结果和椭圆方程很像,但是无法保证我们的M是对角矩阵,先不管为什么要和椭圆扯上关系,我们对M进行特征值分解。
1=[xy][λ12λ22][xy](Ellipse)
M=R−1[λ1λ2]R(Diagonalization of M)
所以,能量函数E(u,v)的值能够被可视化成一个椭圆,λ1,λ2表示两个轴的长度,R表示基旋转的角度。
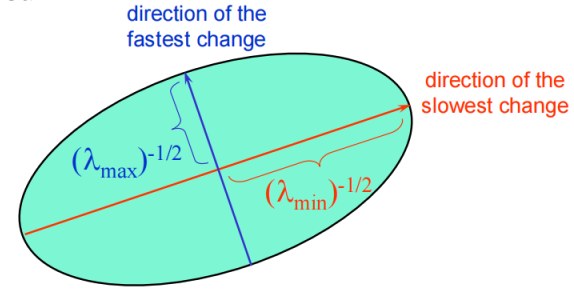
回到我们之前的问题,平坦区域、角点、边的差别就在于能量函数的值,而能量函数的值又取决于这个椭圆,所以,进行统计之后,有下图这种结果。扁扁的椭圆是边,小的圆是平坦区域,大的圆是角点。
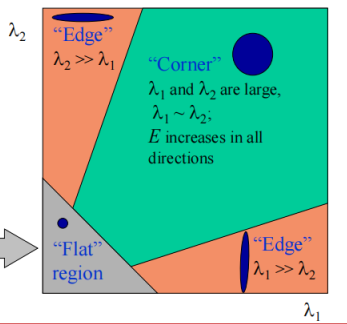
但是要用计算机判断椭圆、计算特征值什么的还是挺困难的,所以接下来大佬进行了一个神操作:
R=λ1λ2−α(λ1+λ2)2=det(M)−α trace(M)2
其中α一般取0.04~0.06。当λ1,λ2都比较大时,乘积比较大,相加比较小,所以R比较大;当λ1,λ2有一个远大于另一个时,相乘就比较小,而大数的平分就比较大,所以R小于0;而当λ1,λ2都很小时,那也显然R比较小。我们判断R和0的关系就能求解。只用再设置一个阈值来区分角点和平坦区域就行了。
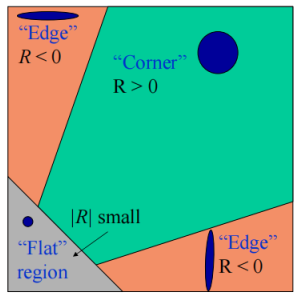
并且,用这个式子我们发现可以和行列式和矩阵的迹扯上关系,刚才分析了半天的特征值也没有必要计算了,因为行列式和矩阵的迹能直接从M矩阵中得到,十分方便。
总结Harris角点检测方法
- 计算图像两个方向的偏导
- 用偏导和额外添加的一个窗函数w(x,y)来计算矩阵M
- 计算角点响应R,并根据阈值找到角点
- 非最大化抑制减少一些重复
不变性分析
- 整体亮度:影响不大,因为计算M矩阵的时候用到的是微分。
- 物体位置改变:影响不大,因为是局部特征。
- 旋转:有一些影响,旋转之后也能找到,但是特征不一样。
- 尺度缩放:有比较大的影响,比如圆角矩形远着看有角,细看就没角了。
- 对比度:有一些影响,因为可能有新的点出现或一些微弱点小消失。
Python实现
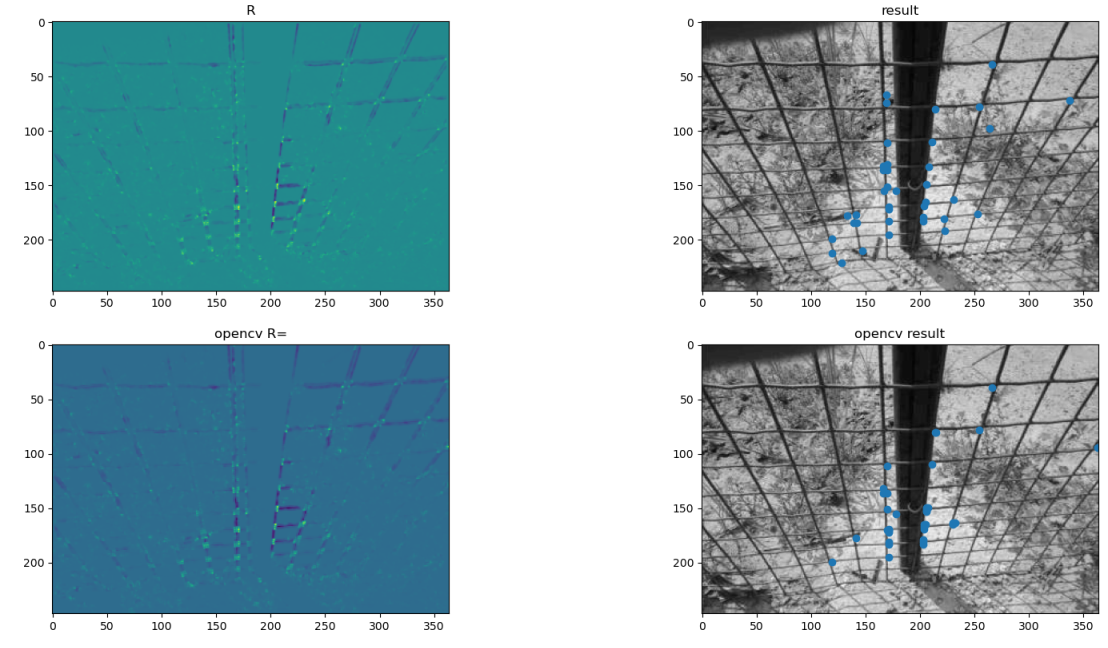
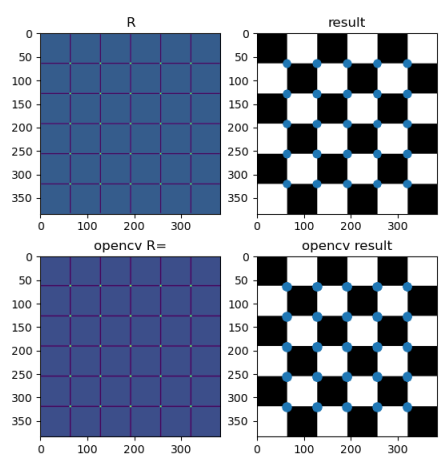
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| import numpy as np
import matplotlib.pyplot as plt
import cv2
def non_max_suppression(x):
res = np.zeros_like(x)
for i in range(x.shape[0]):
for j in range(x.shape[1]):
if x[i, j] == 0:
continue
if np.sum(x[i - 1:i + 2, j - 1:j + 2] > x[i, j]) == 0:
res[i, j] = x[i, j]
return res
img = cv2.imread("imgs/ironnet_small.jpg", cv2.IMREAD_GRAYSCALE)
aperture_size = 3
block_size = 3
alpha = 0.06
r_threshold = 500000
Ix = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=aperture_size)
Iy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=aperture_size)
kernel = np.array([[1, 2, 1], [2, 4, 2], [1, 2, 1]]) / 16
R = np.zeros(img.shape)
for i in range(2, img.shape[0] - 2):
for j in range(2, img.shape[1] - 2):
ix2 = np.sum(Ix[i - 1:i + 2, j - 1:j + 2] ** 2 * kernel)
iy2 = np.sum(Iy[i - 1:i + 2, j - 1:j + 2] ** 2 * kernel)
ixiy = np.sum(Ix[i - 1:i + 2, j - 1:j + 2] * Iy[i - 1:i + 2, j - 1:j + 2] * kernel)
r = (ix2 * iy2 - ixiy ** 2) - alpha * (ix2 + iy2) ** 2
R[i, j] = r
res = non_max_suppression(R)
points = np.where(res > res.max()*0.5)
plt.subplot(2, 2, 1)
plt.imshow(R)
plt.subplot(2, 2, 2)
plt.imshow(img, cmap=plt.get_cmap('gray'))
plt.scatter(points[1], points[0])
plt.subplot(2, 2, 3)
cv2_res = cv2.cornerHarris(img, 3, 3, alpha)
plt.imshow(cv2_res)
plt.subplot(2, 2, 4)
cv2_points = np.where(cv2_res > cv2_res.max()*0.5)
plt.imshow(img, cmap=plt.get_cmap('gray'))
plt.scatter(cv2_points[1], cv2_points[0])
plt.show()
|
尺度不变检测
Harris角点检测虽然有用,但是假如图片进行了尺度缩放,就可能无法检测到对应的点了,所以我们还需要一个尺度不变的特征点提取方式(Blob Detection)。
从高斯到拉普拉斯
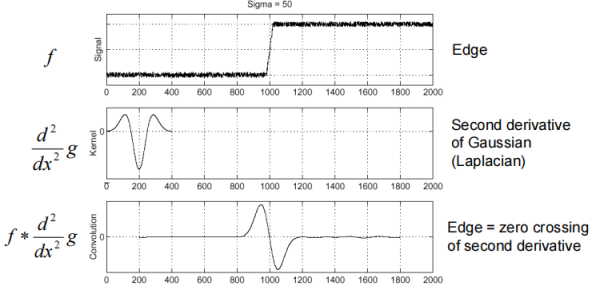
那么如何进行尺度的检测呢?我们先来了解**拉普拉斯核(Laplacian)**的一个有趣的性质。拉普拉斯核,其实也就是高斯核求两次导,能较好地得到下图第三行的这种结果,过零点是边缘位置。
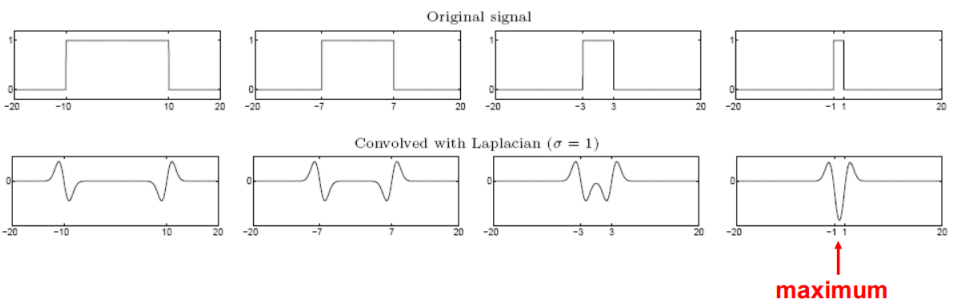
接下来看这张比较重要的图,左边第一二列能够比较明显检测出两个边缘,而当这个慢慢变瘦的时候,用拉普拉斯核卷积出来的响应会慢慢融合,直到缩放到某个程度的时候,两个响应合在一起会得到一个最大值。此时,我们称拉普拉斯模版和信号匹配上了,也就是用不同的拉普拉斯模版检测到了信号的尺度。
但是这个有小问题,就是刚才固定的是拉普拉斯的σ,现实中固定的是图像尺度,而改变σ的时候会发现拉普拉斯信号会变平,所以要乘回个σ2。下图尺度和σ=8有关系,然而没有标准化的时候信号几乎都看不到了。

从σ到尺度
既然有了拉普拉斯这种方法,我们就可以开始准备检测尺度了。
对于一个图像,我们可以用许多不同σ的拉普拉斯核进行卷积,然后就会得到H×W×C的一个数组,里面的值代表该像素在某个σ下的响应。要找到极值,我们可以进行非最大化抑制,判断3×3×3范围内其他值是否大于中心值,假如中心值是最大的,那就找到了一个点和对应的σ。在检测出了σ之后,我们就能画出一个半径为3σ的圆表示检测结果了(3σ是经验公式)。

然而,根据我们现在的方法,图像的每一个像素都要进行处理,而且要用很大的卷积核,太耗费资源了,所以我们要想办法减少复杂度:
- 第一种方法是结合Harris角点,在检测出角点的周围像素进行检测,而不是对所有像素都进行多尺度的滤波。
- 第二种方法就是著名的SIFT。
SIFT
SIFT(Scale-Invariant Feature Transform)是尺度不变特征变换,这种方法使用DoG(Difference of Gaussians)来代替拉普拉斯核。DoG的定义如下,是对图像进行不同σ的高斯的差。
DoG=G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2Laplacian∇2G(σ)
**推导:**本质上是差分近似代替微分
∂σ∂G≈(k−1)σG(kσ)−G(σ)
而恰巧
∂σ∂G=σ5−2σ2+x2+y2exp(−2σ2x2+y2)∇2G=σ6−2σ2+x2+y2exp(−2σ2x2+y2)∴∂σ∂Gσ=∇2G
那么究竟是怎么减少计算量的呢?高斯函数有一个特别的性质,两个一维高斯函数的卷积还是高斯函数,且能算出标准差σ:G1(x,σ1)∗G2(x,σ2)=G(x,σ12+σ22)(证明见2003-003.dvi (psu.edu))。高斯函数还有一个特别的性质,一个二维高斯函数可以拆分成两个方差相同的一维高斯函数的卷积:I(x,y)∗g(x,y)=I(x,y)∗gcolumn(y)∗grow(x)(证明见二维高斯核的可分离性)。这两个性质何在一起,对一幅图像进行σ=1的高斯平滑后,再对平滑后的图像进行一次σ=1的高斯平滑,结果和直接进行σ=2的高斯平滑等价。也就是说,大σ能够分解成多个小σ。
如下图,左边从下往上依次是σ,kσ,k2σ,k3σ,k4σ,计算完第一层后,对第一层的图像进行一次σk2−1的高斯平滑就能得到第二层,所以能减少实际计算高斯平滑所用的σ的值,也就是不用那么宽的窗了。而得到左边黄色的一叠图像之后,求差值就能得到右边蓝色的一叠图像。右边蓝色的图像可以直接来找极值。
虽然窗宽的增长速度变慢了,但是在大尺度的时候仍然有过宽的问题,所以SIFT还区分了octave,一个octave就像下图的五个黄色高斯层,在这么一个octave结束之后,图像会缩小到原来的二分之一。之前是通过增加窗宽来增加尺度,现在通过减小图像也能增加尺度,这也是SIFT减少计算量的方式之一。
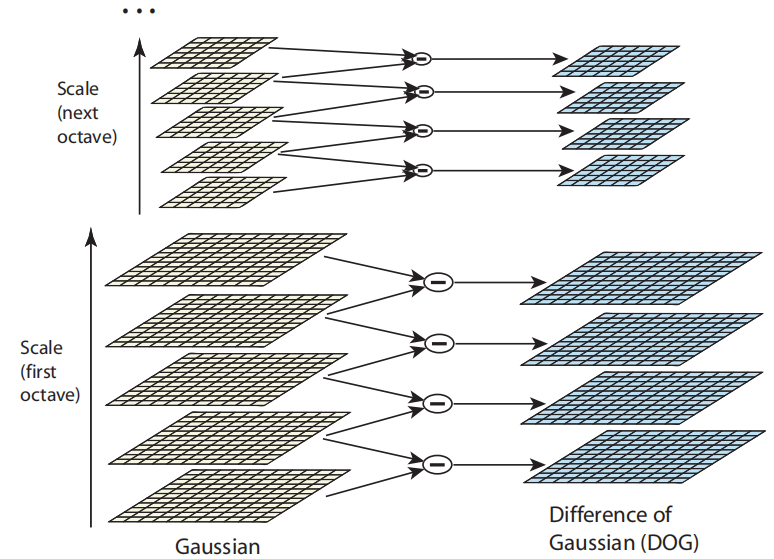
假设一个octave要提取出s个尺度,那么k=21/s,
参考文献:
Harris 角点学习笔记 - 知乎 (zhihu.com)
计算机视觉(本科) 北京邮电大学 鲁鹏 清晰完整合集_哔哩哔哩_bilibili














