线性代数自用超基础笔记

大学课堂上怎么可能听得懂（笑），跟着3Blue1Brown大神学吧！笔记可能不严谨，慎看！

向量是什么？

$\begin{bmatrix}-2\\\\ 3\end{bmatrix}$是一个原点在$(0,0)$，终点在$(-2,3)$的箭头。

$\begin{bmatrix}2\\\\ 1\\\\ 3\end{bmatrix}$是一个原点在$(0,0,0)$，终点在$(2,1,3)$的箭头。

向量可以相加、可以乘常数，表示这个箭头的变化。

单个向量看做箭头比较合适

多个向量看做点比较合适

基向量

二维空间中有两个特殊的向量$\hat{i},\hat{j}$，叫做基向量（basis vectors）。其它向量也可以表示成基向量乘常数然后相加，比如$\begin{bmatrix}-2\\\\ 3\end{bmatrix}$是$\hat{i}$乘常数-2，$\hat{j}$乘常数3之后相加。

线性相关 线性无关

那假如我们选择另外两个向量当做基向量呢？显然，只要选择两个线性无关（Linearly independent）（不共线）的向量作为基向量，那就可以张成一个二维空间。假如线性相关（Linearly dependent），那就只能张成一条直线。更高维的空间同理。

矩阵乘法与线性变换（Linear Transformation）

“变换”类似于一个“函数”，输入进一个向量，输出一个向量，而用“变换”这一次的原因是需要我们从运动的角度看待，即输入向量运动到输出向量上。而考虑整个变换，则要考虑空间内所有向量经过变换后到达对应的另一个向量。

而线性变换指的是直线在变换之后仍然是直线，且原点固定。

如何表示线性变换呢？只需要记录两个基向量变换后的位置就行。下面是一个例子，其中$\hat{i}$变换到了$(3,-2)$，而$\hat{j}$变换到了$(2,1)$。我们通常用矩阵来表示：$\begin{bmatrix}3&2\\\\ -2&1\end{bmatrix}$。

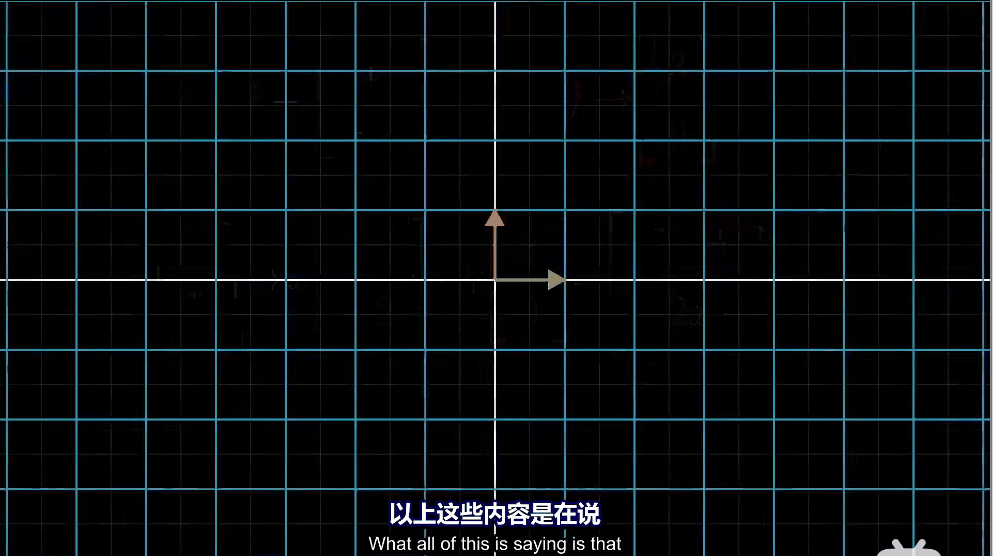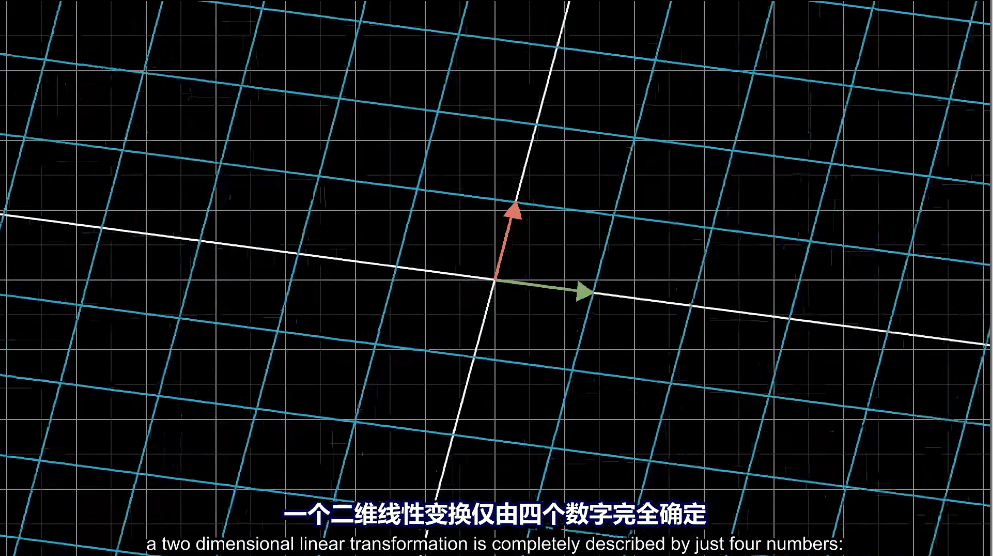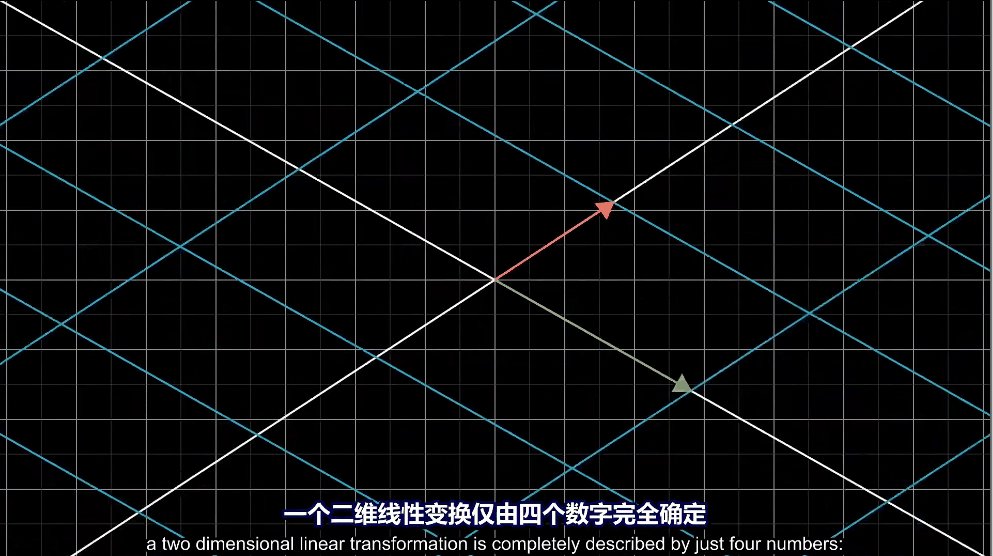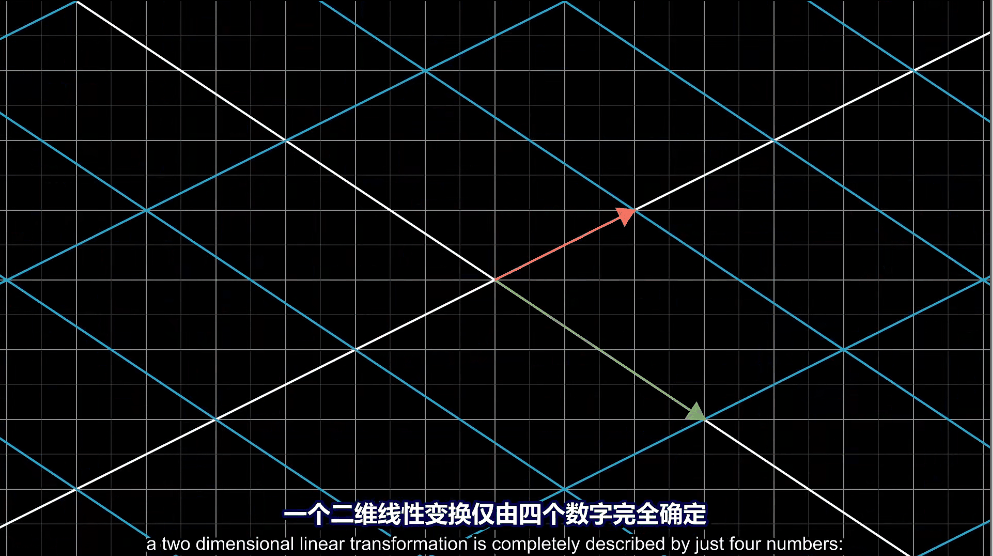
而矩阵乘法就能表示对某一个向量进行线性变换：

$$\begin{bmatrix}a&b\\\\ c&d\end{bmatrix}\begin{bmatrix}x\\\\ y\end{bmatrix}$$

行列式

既然矩阵能变换空间，我们来关注一下面积的变化：原空间中面积为1的区域变换后的面积就叫做行列式（determinant）。当变换后面积为0时，变换后的基肯定是线性相关的了。当变换的面积是负数时，其实是把空间翻了个面。

2x2的行列式很好算，就是左上乘右下减去右上成左下。

$$def(\begin{bmatrix}3&2\\\\ 0&2\end{bmatrix})=6$$

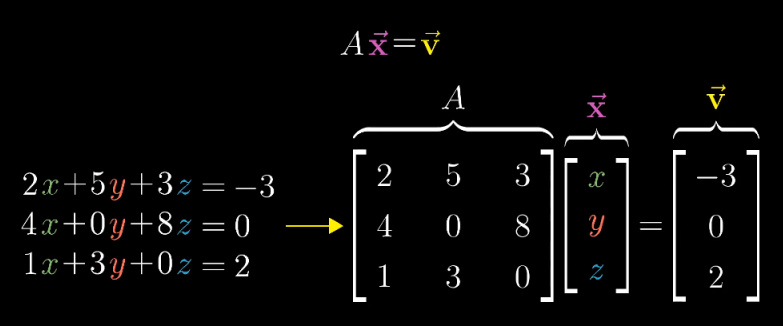
线性方程组与矩阵

线性方程组可以按照下面的方式写成矩阵，要求解就是找到一个向量$\vec{x}$，使用$A$变换后能变到$\vec{v}$上。

逆矩阵（inverse）

既然矩阵$A$能让$\vec{x}$变换到$\vec{v}$，那也会有另一个矩阵让$\vec{v}$变换到$\vec{x}$，即$\vec{x}=A^{-1}\vec{v}$，这就是矩阵的逆。

显而易见，$A^{-1}A=AA^{-1}=E$，先变过去再变回来还是原来的基向量。

矩阵的逆存在的条件是行列式不为零$det(A)\neq0$，因为被压缩成直线以后不能在变回来。

秩（Rank）

一个矩阵变换后空间的维数

基变换 相似矩阵

现在有两个空间，我们可以用矩阵乘来将A空间的向量转换到B空间，但假如我想对A空间进行一个变换（旋转90°），那我要怎么得到这个变换在B空间的表示呢？

假设$M$是我想要表示的变换，而$A$能够让一个向量从A空间变换到B空间，那么$M$在B空间的表示为：$A^{-1}MA$。

而且，$A^{-1}MA$和$M$是相似矩阵。

特征值 特征向量（Eigenvalue Eigenvector）

某个矩阵$A$满足$\boldsymbol{A}\vec{v}=\lambda\vec{v}$时，$\vec{v}$是特征向量，$\lambda$是特征值。

也就是说这个矩阵对向量$\vec{v}$变换后，不改变方向，只改变长度到$\lambda$倍。

解法就是移项到左边$(\boldsymbol{A}-\lambda\boldsymbol{I})\vec{v}=0$，默认特征向量不为0，那么就是求让特征向量在变换后是零向量的矩阵，即$det(\boldsymbol{A}-\lambda\boldsymbol{I})=0$。

特别的，对角矩阵的对角元就是特征值。

特征值分解

结合基变换，我们可以对相似矩阵进行特征值分解。一个线性变换可以看作是旋转+拉伸，特征值分解就是把旋转和拉伸分开。对于某个矩阵$\boldsymbol{A}$，分解成

$$A=P\Lambda P^{-1}$$

其中P是表示旋转变换（基变换），且列向量是单位化的特征向量。而$\Lambda$是对角矩阵，表示拉伸变换，对角元是特征值。

其实反过来就是$P^{-1}AP=\Lambda $，就是当前这个矩阵在另一个对基向量表示的空间下是对角矩阵。