密码学 消息认证码（MAC）与散列函数（hash 哈希函数） 附代码

密码学 消息认证码（MAC）与散列函数（hash）

**消息认证码（MAC，Message Authentication Code）**能够使用一个密钥K来浓缩一个任意长的消息M，数学表示为$MAC=C_K(M)$。易知MAC是一种多对一的函数，主要用来使通信双方确信消息内容未被更改。MAC需要保证：

• 假如某人已知消息$M$和$C_K(M)$，也无法构造$M'$使$C_K(M')=C_K(M)$。
• 假如改变$M$的一个或多个bit，消息认证码相同概率极低
• 任意两个消息的消息认证码相同概率极低

消息认证码的实现算法中，通常使用散列函数（hash function）实现，这种实现方法统称散列消息认证码（HMAC）。常用的散列函数包括：SHA-1、SHA-256、MD5。

HMAC

HMAC在RFC2104中定义如下，其中$\oplus$是异或XOR，$||$是拼接。

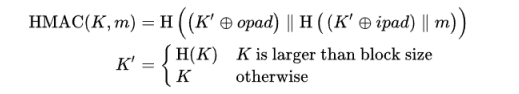
公式有点抽象，我画了个图。一开始要将密钥$K$得到$K'$，即把不定长的密钥通过补0或者hash得到定长的b bit密钥，这里的$b$是hash函数的分块大小。得到$K'$之后，需要和一个常数ipad进行异或，ipad是0x36的二进制循环重复。异或之后得到$S_i$，和消息进行拼接后送入Hash处理得到n bit，这里的$n$是hash函数的输出长度。之后和前面再进行一次类似的操作，就能得到最终结果。

散列函数 HASH

所有散列函数都有如下一个基本特性：如果两个散列值是不相同的（根据同一函数），那么这两个散列值的原始输入也是不相同的。但是假如不同的输入得到了相同的输出，就发生了**“散列碰撞”**。

散列函数的输入一般是非常非常大的，可以将消息分块hash，输出值域是固定的。

算法名称	block大小	输出大小
MD5	512	128
SHA-0	512	160
SHA-1	512	160
SHA-256	512	256
SHA-512	1024	512

MD5原理

1. 对消息进行填充

   满足填充后长度mod 512 = 448，留出64bit表示原始信息长度。

   填充方法是先填充一个1，然后全填充0。

   填充是必须存在的，假如长度是是960mod512=448，那也需要填充512bit。

   由于理论上信息无限长，所以表示信息长度的64bit进行取模循环使用。

2. 分组

   将上面的数据分成512bit的block$\boldsymbol {M}$，然后每个block细分成16个32bitword，第$i$个word用$\boldsymbol {M_i}$表示。

3. 获取常数表$\boldsymbol T$

   $\boldsymbol T$中一共有64个元素，每个元素是32bit的数字，由下面公式算出：

   $\boldsymbol T_i = int(4294967296 \times abs(\sin(i)))$

4. 规定辅助函数F G H I

   定义4个辅助函数如下：

   $$F(X,Y,Z)=(XY)\lor ((\neg X)Z)$$

   $$G(X,Y,Z)=(XZ)\lor (Y(\neg Z))$$

   $$H(X,Y,Z)=X \oplus Y \oplus Z$$

   $$I(X,Y,Z)=Y \oplus (X\lor\neg Z)$$

5. 初始化寄存器A B C D

   初始化A、B、C、D四个32bit的寄存器，初始值如下：

   A: 01 23 45 67
   B: 89 ab cd ef
   C: fe dc ba 98
   D: 76 54 32 10

6. 进行运算

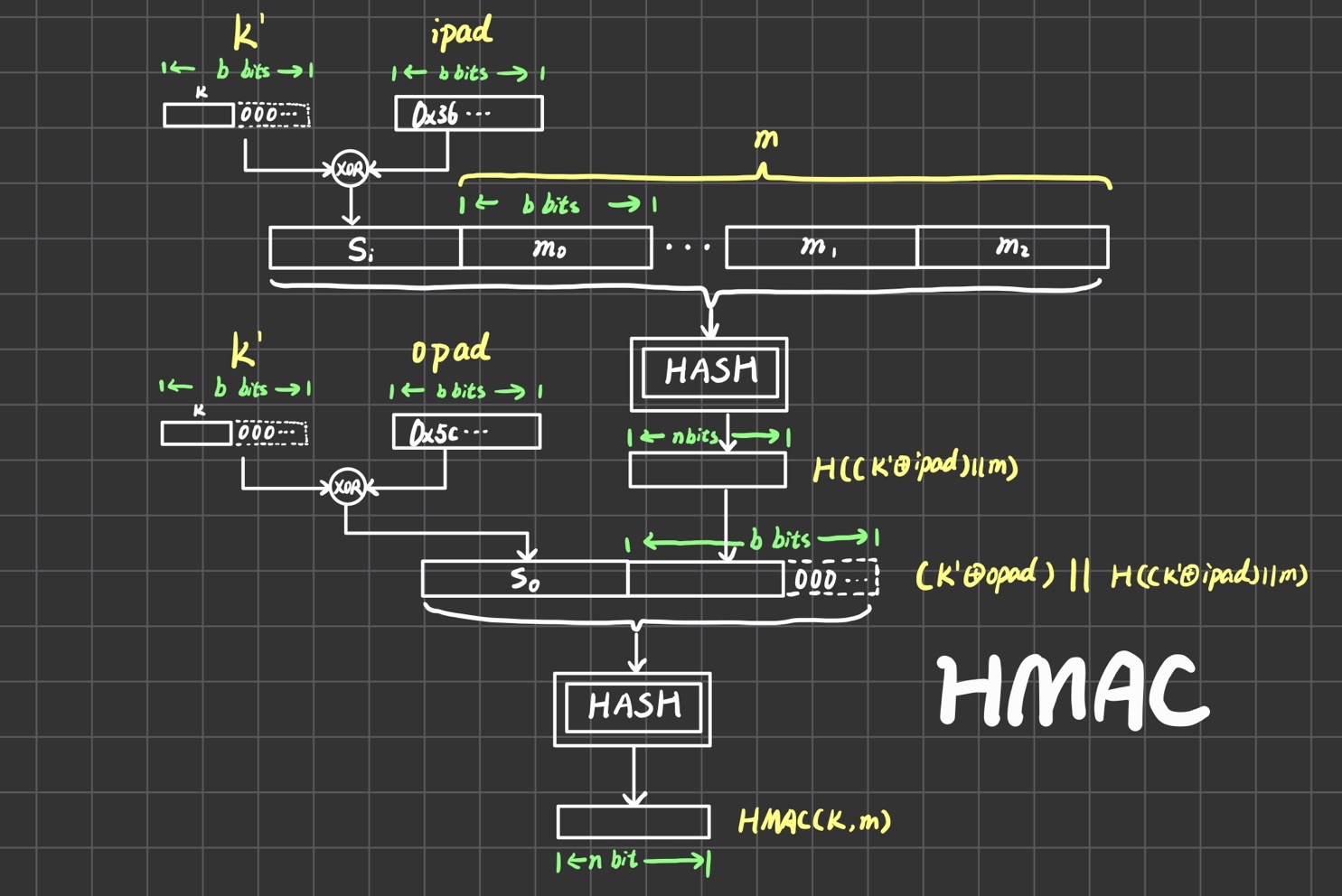
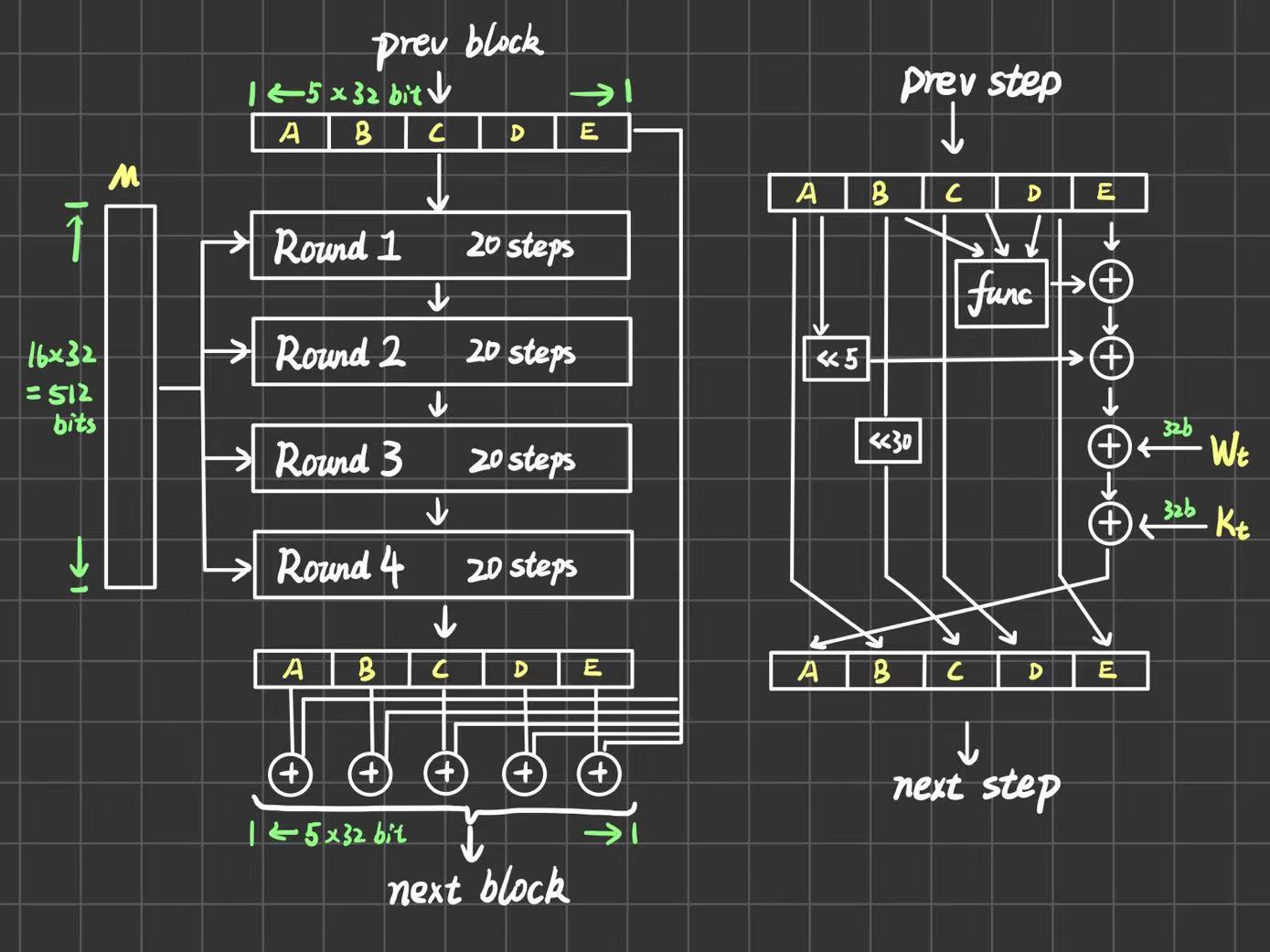
   整体结构如下图，上一个block的输出作为当前block的输入（首个输入就用第5步的初始化），每一个block进行4轮运算，每轮运算又分成16步。在4轮结束之后，ABCD寄存器的值要和输入的ABCD寄存器值分别进行一个模32bit求和。

   

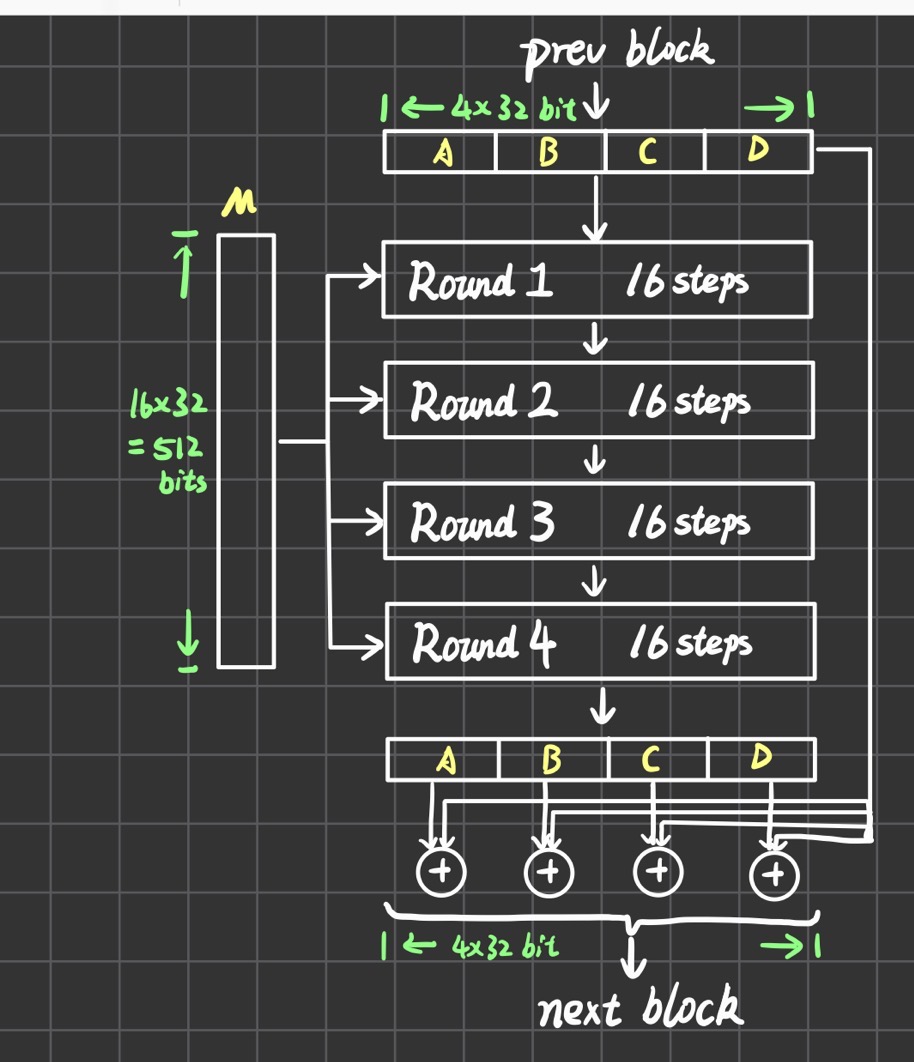
   每一步的具体情况如下图，图中func表示每一轮用到的辅助函数，就是第4点的FGHI，四个辅助函数分别对应4轮。图中所有的加法都是模32bit，<<表示循环左移s位。每一步需要三个参数i,j,s。这三个参数的确定如下：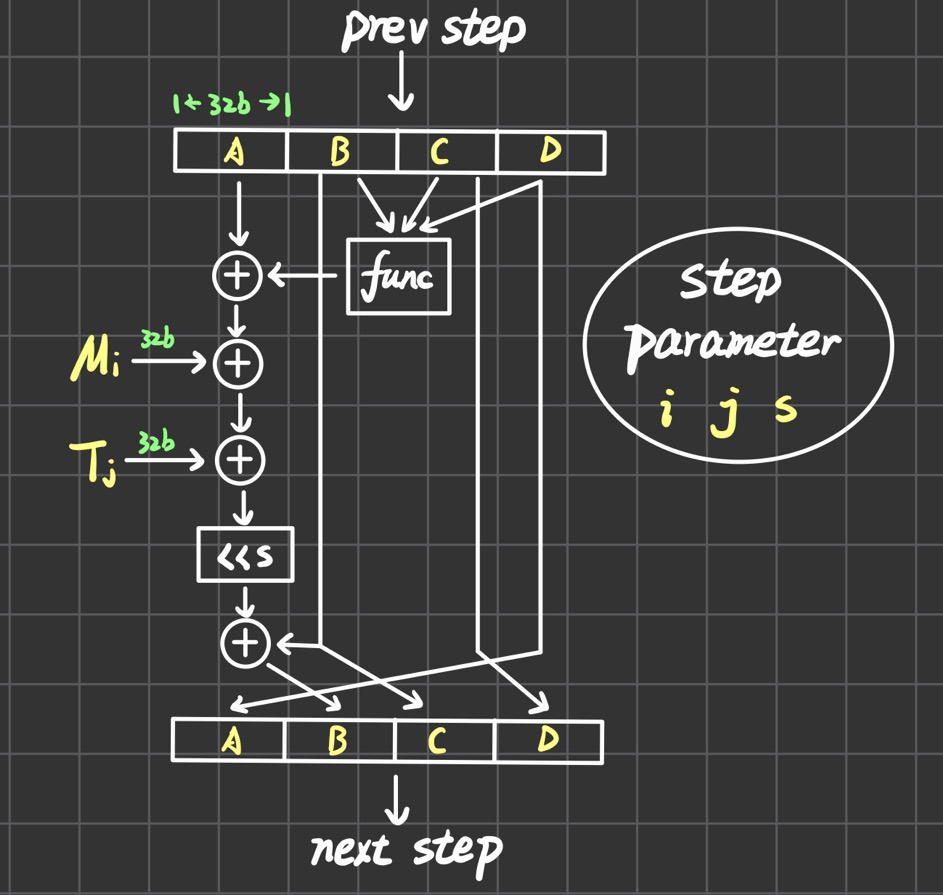

   

   • i

     设某一轮中第$k$步

     第一轮：$i=k$；

     第二轮：$i=(1+5k)mod16$；

     第三轮：$i=(5+3k)mod16$；

     第四轮：$i=(7k)mod16$；

   • j

     四轮总共有64步，从这个角度的第$j$步。

   • s

     第一轮：7 12 17 22循环使用

     第二轮：5 9 14 20循环使用

     第三轮：4 11 16 23循环使用

     第四轮：6 10 15 21循环使用

MD5实现

使用Python根据RFC1321.txt实现的MD5算法，转载请保留署名。

最新代码在GitHub维护

需要注意的是字节序！对应reverse_endianness这个函数。

比如用4Byte保存的数字8本来是00 00 00 08，但是翻转字节序之后就是08 00 00 00了。

算法中的寄存器初始值、信息长度、block信息和最后寄存器输出都要改变一下字节序。

# -*- coding: utf-8 -*-
#
# coded by Kamino, 2022, <kamino@cuc.edu.cn>
#
# It is a simple implementation of the MD5 algorithm in Python3.10.
# Distributed freely with attribution.
# This code is based on rfc1321.txt.
# It is not recommended to use this code in practice. For security
# and performance, please use hashlib.
#
import bitarray as ba
from bitarray.util import ba2int, int2ba, hex2ba
from typing import Union
import hashlib  # Only for evaluation


class MD5:
    # Constants
    T = [
        0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
        0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
        0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x2441453, 0xd8a1e681, 0xe7d3fbc8,
        0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
        0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
        0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x4881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
        0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
        0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391,
    ]
    # index of message word(32b)
    MI = [
        [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
        [1, 6, 11, 0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12],
        [5, 8, 11, 14, 1, 4, 7, 10, 13, 0, 3, 6, 9, 12, 15, 2],
        [0, 7, 14, 5, 12, 3, 10, 1, 8, 15, 6, 13, 4, 11, 2, 9],
    ]
    # shift numbers
    S = [
        [7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, ],
        [5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, ],
        [4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, ],
        [6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, ]
    ]
    # initial numbers of the 4 register
    INIT = [0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476]
    # functions
    F = lambda x, y, z: (x & y) | ((~x) & z)
    G = lambda x, y, z: (x & z) | (y & (~z))
    H = lambda x, y, z: x ^ y ^ z
    I = lambda x, y, z: y ^ (x | (~z))

    @classmethod
    def hash(cls, src: Union[bytes, str]) -> str:
        processed_blocks = cls._preprocess(src)
        res = cls.md5_core(processed_blocks)
        return res.tobytes().hex()

    @classmethod
    def reverse_endianness(cls, x: ba.bitarray) -> ba.bitarray:
        """
        Change the endianness of x.
        example when x is a number of 264:
        00 00 00 00 00 00 01 08 -> 08 01 00 00 00 00 00 00
        :param x:
        :return:
        """
        _x = x.tobytes().hex('_').split('_')
        _x.reverse()
        return hex2ba("".join(_x))

    @classmethod
    def _preprocess(cls, src: Union[bytes, str]):
        """
        Make blocks of 512bit/64B and pad to the standard format
        :param src:
        :return:
        """
        src = src.encode() if type(src) is str else src
        length = len(src)
        # make blocks
        blocks = []
        for i in range(0, len(src), 64):
            block = ba.bitarray()
            block.frombytes(src[i: i + 64])
            blocks.append(block)

        # pad 100...0
        if len(blocks) == 0:  # prevent empty input
            blocks.append(ba.bitarray())
        if len(blocks[-1]) < 448:  # less than 488bit: pad 100...0 until 488
            blocks[-1].extend("1" + "0" * (448 - len(blocks[-1]) - 1))
        elif len(blocks[-1]) < 512:  # greater than or equal to 488：pad to 512，than add a new block of 448*0
            blocks[-1].extend("1" + "0" * (512 - len(blocks[-1]) - 1))
            blocks.append(ba.bitarray("0" * 448))
        else:  # equal to 512，directly add a padded block of 488
            blocks.append(ba.bitarray("1" + "0" * 447))

        # add the 64bit/8B length to the end
        # NOTICE! low-order bytes are placed earlier
        # example when length is 264:
        # 00 00 00 00 00 00 01 08 -> 08 01 00 00 00 00 00 00
        blocks[-1] += cls.reverse_endianness(int2ba(length * 8, 64))
        return blocks

    @classmethod
    def _cyclic_left_shift32(cls, x, n):
        """Cyclic left shift n bit of a 32bit word"""
        # & 0xffffffff means (mod 2^32)
        return ((x << n) | (x >> (32 - n))) & 0xffffffff

    @classmethod
    def _step(cls, a, b, c, d, mi, tj, s, func):
        """process a step."""
        # & 0xffffffff means (mod 2^32)
        e1 = (func(b, c, d) + a + mi + tj) & 0xffffffff
        e2 = (b + cls._cyclic_left_shift32(e1, s)) & 0xffffffff
        return d, e2, b, c

    @classmethod
    def md5_core(cls, blocks):
        """
        Core function of MD5 algorithm.
        Notice the to reverse endianness!
        """
        func_list = (cls.F, cls.G, cls.H, cls.I)
        a, b, c, d = cls.INIT
        # Block
        for block in blocks:
            aa, bb, cc, dd = a, b, c, d
            # Round
            for round_num in range(4):
                # Step
                for step_num in range(16):
                    block_bytes = block[cls.MI[round_num][step_num] * 32:cls.MI[round_num][step_num] * 32 + 32]
                    aa, bb, cc, dd = cls._step(
                        aa, bb, cc, dd,
                        ba2int(cls.reverse_endianness(block_bytes)),
                        cls.T[round_num * 16 + step_num],
                        cls.S[round_num][step_num],
                        func_list[round_num]
                    )
            a = (a + aa) & 0xffffffff
            b = (b + bb) & 0xffffffff
            c = (c + cc) & 0xffffffff
            d = (d + dd) & 0xffffffff
        return cls.reverse_endianness(int2ba(a, 32)) + cls.reverse_endianness(int2ba(b, 32)) + \
               cls.reverse_endianness(int2ba(c, 32)) + cls.reverse_endianness(int2ba(d, 32))


test_suite = {
    "": "d41d8cd98f00b204e9800998ecf8427e",
    "a": "0cc175b9c0f1b6a831c399e269772661",
    "abc": "900150983cd24fb0d6963f7d28e17f72",
    "message digest": "f96b697d7cb7938d525a2f31aaf161d0",
    "abcdefghijklmnopqrstuvwxyz": "c3fcd3d76192e4007dfb496cca67e13b",
    "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789": "d174ab98d277d9f5a5611c2c9f419d9f",
    "12345678901234567890123456789012345678901234567890123456789012345678901234567890": "57edf4a22be3c955ac49da2e2107b67a"
}

for k, v in test_suite.items():
    # my_res = md5(md5_pad(str2bin(k))).tobytes().hex()
    my_res = MD5.hash(k)
    hashlib_res = hashlib.md5(k.encode()).hexdigest()
    truth_res = v
    print(f"For message: \"{k}\"")
    print(f"My: {my_res}\nHashlib: {hashlib_res}\nTruth: {truth_res}")
    print(f"\033[1;33;40m {my_res == hashlib_res == truth_res} \033[0m")

SHA1原理

SHA1和MD5整体流程极为相似，输出不同长度的原因是MD5是有ABCD四个32bit的寄存器，而SHA1有ABCDE五个32bit的寄存器，所以输出是160bit。

1. 填充

   和MD5一模一样，填充到448bit，然后附加64bit的表示长度的整数

2. 分组

   也和MD5一模一样，将上面的数据分成512bit的block$\boldsymbol {M}$，然后每个block细分成16个32bitword，第$i$个word用$\boldsymbol {M_i}$表示。

3. 获取常数$\boldsymbol{K}$

   只有4个数，但是整个数组有80个位置，对应80step。

   \displaylines{K_{0-19}=5A827999\\\\ K_{20-39}=6ED9EBA1\\\\ K_{40-59}=8F1BBCDC\\\\ K_{60-79}=CA62C1D6 }

4. 规定辅助函数

   和MD5很像也有4个辅助函数，每个函数负责一个Round。其实可以发现第二和第四是一样的。

   \displaylines{F_1(X,Y,Z)=(XY)\lor ((\neg X)Z)\\\\ F_2(X,Y,Z)=X\oplus Y\oplus Z\\\\ F_3(X,Y,Z)=(XY)\lor(XZ)\lor(YZ)\\\\ F_4(X,Y,Z)=X\oplus Y\oplus Z }

5. 初始化寄存器ABCDE

   5个32bit的寄存器，注意下面写的字节序是倒着的，直接赋值应该是A=0x67452301

   A: 01 23 45 67
   B: 89 ab cd ef
   C: fe dc ba 98
   D: 76 54 32 10
   E: f0 e1 d2 c3

6. 进行运算

   总共有4Round，每个Round有20step，用$t$表示总步数。和MD5一样，下面的$\oplus$都是$mod\ 2^{32}$的加法，$<<$都是循环左移，func是之前提到的辅助函数。和MD5不一样的是，每一步只有一个$t$参数，在$t \leq 15$时，$W_t$不变，当$t\ge16$时，$W_t=(W_{t-3} \oplus W_{t-8} \oplus W_{t-14} \oplus W_{t-16})<<1$。

   

SHA1实现

和MD5实现差不多，但是完全不需要考虑字节序。转载请署名。

最新代码维护于GitHub

# -*- coding: utf-8 -*-
#
# coded by Kamino, 2022, <kamino@cuc.edu.cn>
#
# It is a simple implementation of the MD5 algorithm in Python3.10.
# Distributed freely with attribution.
# This code is based on FIPS PUB 180-1 SECURE HASH STANDARD.
# It is not recommended to use this code in practice. For security
# and performance, please use hashlib.
#
import bitarray as ba
from bitarray.util import ba2int, int2ba, hex2ba
from typing import Union
import hashlib  # Only for evaluation


class SHA1:
    # Constants
    K = [0x5A827999] * 20 + [0x6ED9EBA1] * 20 + [0x8F1BBCDC] * 20 + [0xCA62C1D6] * 20
    # initial numbers of the 5 register
    INIT = [0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476, 0xc3d2e1f0]
    # functions
    F1 = lambda x, y, z: (x & y) | ((~x) & z)
    F2 = lambda x, y, z: x ^ y ^ z
    F3 = lambda x, y, z: (x & y) | (x & z) | (y & z)
    F4 = lambda x, y, z: x ^ y ^ z

    @classmethod
    def hash(cls, src: Union[bytes, str]) -> str:
        processed_blocks = cls._preprocess(src)
        res = cls.sha1_core(processed_blocks)
        return res.tobytes().hex()

    @classmethod
    def _preprocess(cls, src: Union[bytes, str]):
        """
        Make blocks of 512bit/64B and pad to the standard format
        :param src:
        :return:
        """
        src = src.encode() if type(src) is str else src
        length = len(src)
        # make blocks
        blocks = []
        for i in range(0, len(src), 64):
            block = ba.bitarray()
            block.frombytes(src[i: i + 64])
            blocks.append(block)

        # pad 100...0
        if len(blocks) == 0:  # prevent empty input
            blocks.append(ba.bitarray())
        if len(blocks[-1]) < 448:  # less than 488bit: pad 100...0 until 488
            blocks[-1].extend("1" + "0" * (448 - len(blocks[-1]) - 1))
        elif len(blocks[-1]) < 512:  # greater than or equal to 488：pad to 512，than add a new block of 448*0
            blocks[-1].extend("1" + "0" * (512 - len(blocks[-1]) - 1))
            blocks.append(ba.bitarray("0" * 448))
        else:  # equal to 512，directly add a padded block of 488
            blocks.append(ba.bitarray("1" + "0" * 447))

        blocks[-1] += int2ba(length * 8, 64)
        return blocks

    @classmethod
    def _cyclic_left_shift32(cls, x, n):
        """Cyclic left shift n bit of a 32bit word"""
        # & 0xffffffff means (mod 2^32)
        return ((x << n) | (x >> (32 - n))) & 0xffffffff

    @classmethod
    def _step(cls, a, b, c, d, e, wt, kt, func):
        """process a step."""
        # & 0xffffffff means (mod 2^32)
        e = (func(b, c, d) + cls._cyclic_left_shift32(a, 5) + wt + kt + e) & 0xffffffff
        return e, a, cls._cyclic_left_shift32(b, 30), c, d

    @classmethod
    def sha1_core(cls, blocks):
        """
        Core function of SHA1 algorithm.
        Notice the to reverse endianness!
        """
        func_list = (cls.F1, cls.F2, cls.F3, cls.F4)
        a, b, c, d, e = cls.INIT
        # Block
        for block in blocks:
            aa, bb, cc, dd, ee = a, b, c, d, e
            words = [ba2int(block[i * 32:(i + 1) * 32]) for i in range(16)]
            # Global step
            for t in range(80):
                if t >= 16:
                    words.append(cls._cyclic_left_shift32(
                        words[t - 3] ^ words[t - 8] ^ words[t - 14] ^ words[t - 16], 1
                    ))
                aa, bb, cc, dd, ee = cls._step(
                    aa, bb, cc, dd, ee,
                    words[t],
                    cls.K[t],
                    func_list[t // 20]
                )
            a = (a + aa) & 0xffffffff
            b = (b + bb) & 0xffffffff
            c = (c + cc) & 0xffffffff
            d = (d + dd) & 0xffffffff
            e = (e + ee) & 0xffffffff
        return int2ba(a, 32) + int2ba(b, 32) + int2ba(c, 32) + int2ba(d, 32) + int2ba(e, 32)


test_suite = {
    "": "", "a": "", "abc": "", "message digest": "",
    "abcdefghijklmnopqrstuvwxyz": "",
    "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789": "",
    "12345678901234567890123456789012345678901234567890123456789012345678901234567890": ""
}

for k, v in test_suite.items():
    my_res = SHA1.hash(k)
    hashlib_res = hashlib.sha1(k.encode()).hexdigest()
    print(f"For message: \"{k}\"")
    print(f"My: {my_res}\nHashlib: {hashlib_res}")
    print(f"\033[1;33;40m {my_res == hashlib_res} \033[0m")
# print(hashlib.sha1("abc".encode()).hexdigest())
# print(SHA1.hash("abc"))

参考文献：

HMAC - Wikipedia

Hash Based Message Authentication - YouTube

散列函数 - 维基百科，自由的百科全书 (wikipedia.org)

RFC1321.txt

FIPS PUB 180-1 SECURE HASH STANDARD