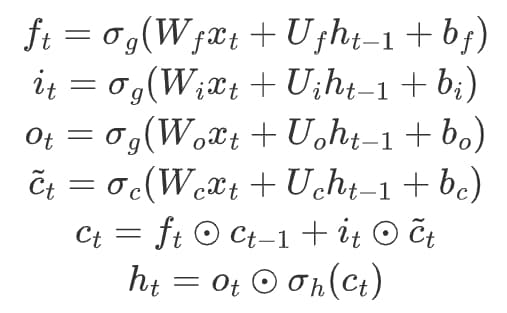论文笔记 RWKV：Reinventing RNNs for the Transformer Era

EMNLP23的一篇文章，一作是Bo Peng，在知乎比较活跃，提出了RWKV模型，其将RNN和Transformer的思想进行结合，使时间复杂度降低到了线性，同时其性能在不同参数量（高达14B）下均得到了验证。

代码链接：BlinkDL/RWKV-LM: RWKV is an RNN with transformer-level LLM performance

RNN ➡️ Transformer➡️Linear Transformer➡️AFT➡️RNN​

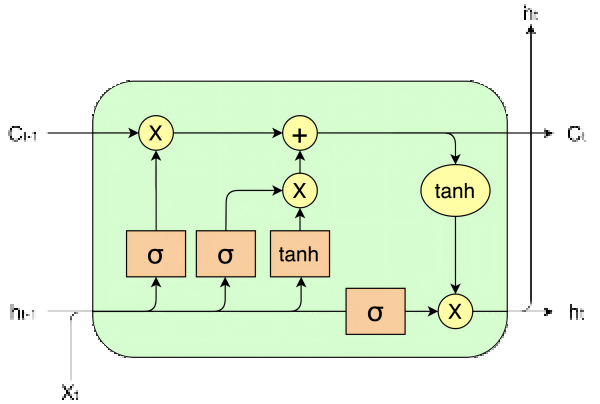
如上图和上式所示是经典RNN——LSTM的架构。

LSTM内部保存hidden和context两种状态，在一次处理中，首先会通过相同的方法，用不同的权重得到4路当前输入和$h$状态的线性变换（前4个式子）。其中，前3路会使用sigmoid函数激活，得到遗忘门$f_t$、记忆门$i_t$和输出门$o_t$，用来作为权重控制遗忘程度、记忆程度和输出程度。

第4路是主要的信息通路，使用tanh函数进行激活，得到当前的信息向量$\tilde{c}_t$。随后，这个信息向量会与之前的$c$状态进行线性组合，用到的就是之前生成的遗忘门和记忆门。这一步得到的结果就是新的$c$状态，由于$c$状态是与之前状态的叠加，所以表示long-term的状态，改变较平缓。

第6个式子则是利用$c$状态+输出门来得到当前的$h$状态，由于其是直接生成的，和$h_{t-1}$没有直接的叠加关系，所以表示short-term的状态，改变较剧烈。

⚠️LSTM类的模型由于依赖前一时刻的输出作为当前输入，所以无法并行，且其保存的状态信息量过少，长期记忆性不好。

✅ 为了解决长期依赖性的问题，Transformer中的自注意力机制带来了全局的点积注意力运算：

$$\text{Attn}(Q,K,V)=\operatorname{softmax}(QK^{\top})V =\frac{\sum^T_{i=1} e^{q_t^{\top} k_i} \odot v_i}{\sum^T_{i=1} e^{q_t^{\top} k_i}} \tag{1}$$

⚠️然而，Transformer的这种机制带来了QK矩阵相乘的平方复杂度，这是我们不想要的

✅所以我们要对注意力机制进行进一步的分析，从论文^[1]中，我们将注意力机制泛化为：

$$\operatorname{attn}_t= \frac{\sum^T_{i=1} \operatorname{sim}(q_t,k_i) \odot v_i}{\sum^T_{i=1} \operatorname{sim}(q_t,k_i)} \tag{2}$$

其中，$\operatorname{sim}(q_t,k_i)$在Transformer中是$\exp (q_t^{\top} k_i)$，而这个操作是可以替换的，只需要保证$\operatorname{sim}: \mathbb{R}^{2\times F} \rightarrow \mathbb{R}_+$。所以，我们可以通过$\phi(x)$来构建这么一个泛化的相似度比较函数（核函数）$\operatorname{sim}(q,k)=\phi(q)^\top \phi(k)$，写到注意力机制中即：

$$\operatorname{attn}_t= \frac{\sum^T_{i=1} \phi(q_t)^\top \phi(k_i) \odot v_i}{\sum^T_{i=1} \phi(q_t)^\top \phi(k_i)} \tag{3}$$

注意分子中三个向量的矩阵乘法可以通过这个规则进行变形：$qkv=(qk)v=q(kv)$，写到注意力机制中即：

$$\operatorname{attn}_t= \frac{\phi(q_t)^\top \sum^T_{i=1} \phi(k_i) \odot v_i}{\phi(q_t)^\top \sum^T_{i=1} \phi(k_i)} \tag{4}$$

经过这个最重要的变形，我们已经将注意力机制的二次复杂度降低到了线性！$(1)$中随着$T$的增长，计算一个$\operatorname{attn}_t$需要进行$2T$个点积，总共需要$T$个输出，所以是$4T^2$个点积，而$(4)$中$\sum^T_{i=1} \phi(k_i) \odot v_i$和$\sum^T_{i=1} \phi(k_i)$在$T$个输出中只需要计算一次，即计算$2T$个点积，然后得到的向量在计算一个$\operatorname{attn}_t$也需要进行$1$个点积，所以总共是$3T$​个点积。

所以，对于线性复杂度的Transformer，我们只需要设计对应的$\phi$​函数即可。

一般情况下，对q使用的$\phi$函数和对k使用的$\phi$函数应该是一样的，具有对称性，但是深度学习时代这个对称性是可以被放松的^[2][3]。

✅ AFT（Attention Free Transformer）就是这种范式下的一种注意力机制

AFT的原型如下：

$$\operatorname{attn}_t= \frac{\sigma(q_t)^\top \sum^T_{i=1} \exp(k_i) \odot v_i}{1(q_t)^\top \sum^T_{i=1} \exp(k_i)} \tag{4}$$

q对应的$\phi$被设计成了一个sigmoid函数和一个常数函数，k对应的$\phi$则设计成了$\exp$函数。

为了考虑位置先验，AFT把key对应的$\phi$加上了一个pair-wise position bias向量：

$$\operatorname{attn}_t= \sigma(q_t) \odot \frac{\sum^t_{i=1} \exp{(w_{t,i} + k_i)} \odot v_i}{\sum^t_{i=1} \exp{(w_{t,i} + k_i)}} \tag{5}$$

然而，由于引入的这个向量包含了与$t$有关的$w_{t,i}$，所以$(5)$并不是线性复杂度的。

✅ 在进行生成式任务时，Transformer往往会施加Causal Masking，成为一个因果的注意力，而论文^[1]发现这和RNN的形式相似：

$$\begin{aligned} s_0 &= 0, z_0 = 0 \\ s_i &= s_{i-1} + \phi(x_iW_K)(x_iW_V)^\top \\ z_i &= z_{i-1} + \phi(x_iW_K), \\ y_i &= \frac{\phi(x_iW_Q)s_i}{\phi(x_iW_Q)z_i} \end{aligned} \tag{6}$$

其中状态包括两部分：$s$叫做attention memory，$z$叫做normalizer memory，分别对应分子和分母，在逐个计算注意力的时候，实际上就是在不断累积这些memory，输出的时候进行最后一行的运算即可得到结果。

✅ RWKV就是这种范式下的一个新模型，其在AFT的基础上，将$w$从一个$T \times T$的矩阵改为一个$T$维向量+位置相关的衰减系数

RWKV

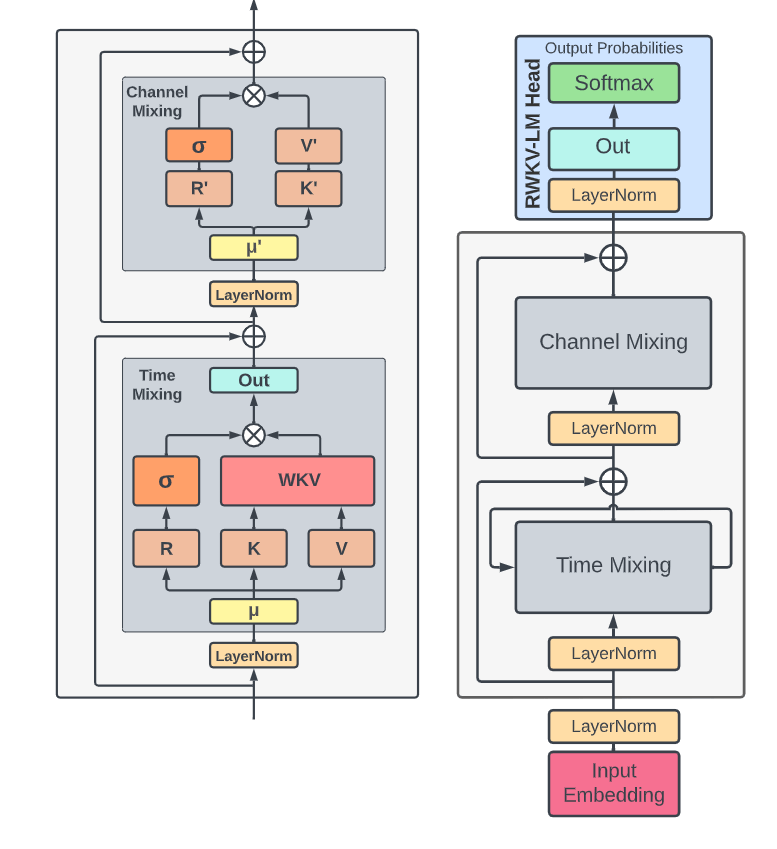
如图是RWKV的整体架构，和Transformer类似（或者说与MLP-mixer类似），token先进行token-level的信息交换（Time Mixing），然后channel-level的信息交换（Channel Mixing）。

RWKV的名称由来如下：

• R：Receptance向量，表示从过去接收的信息（其实和之前介绍过程中泛化的Query类似）
• W：一个可训练的向量，表示根据位置获取信息的参数
• K：和Transformer中的key类似
• V：和Transformer中的value类似

Time-Mixing

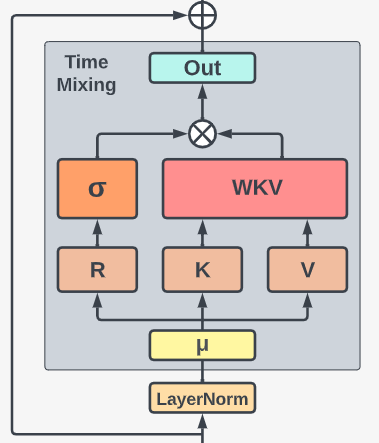
RWKV在mix之前会进行Token shift，time-mixing的输入是当前输入$x_t$和上一步输入$x_{t-1}$的线性组合的线性映射（类似Transformer中生成QKV的过程）：

$$r_t = W_r \cdot (\mu_r \odot x_t + (1-\mu_r) \odot x_{t-1}) \\ k_t = W_r \cdot (\mu_k \odot x_t + (1-\mu_k) \odot x_{t-1}) \\ v_t = W_r \cdot (\mu_v \odot x_t + (1-\mu_v) \odot x_{t-1}) \tag{7}$$

之后，K和V进行WKV算子运算：

$$\begin{aligned} \operatorname{wkv}_t &=\frac {\sum^t_{i=1} e^{-(t-i)w + k_i} \odot v_i} {\sum^t_{i=1} e^{-(t-i)w + k_i}} \\ &=\frac {\sum^{t-1}_{i=1} e^{-(t-1-i)w + k_i} \odot v_i + e^{u+k_t} \odot v_t} {\sum^{t-1}_{i=1} e^{-(t-1-i)w + k_i} + e^{u+k_t}} \\ \end{aligned} \tag{8}$$

其中，第一行和$(5)$比较相似，只不过加上的位置相关的向量改成了channel-wise time decay vector（$w$）与相对位置相乘。作者令$w$是一个d维的大于等于0的向量，从而使$e^{w_{t,i}} \le 1$，使其具有“衰减”的含义。即上式中 $\exp (-(t-i)w + k_i) = \exp (-(t-i)w) \exp (k_i)$，而第一项是一个大于0，小于1的数，随着$t-i$​越大越接近0。第二行是RWKV最终使用的式子，即当$t=i$时，本来是加上0乘$w$，但是不太好，所以加上了另一个可学习的向量$u$。

在得到结果之后，利用$r_t$进行类似LSTM的输出门控：

$$o_t = W_o \cdot (\sigma(r_t) \odot \operatorname{wkv}_t) \tag{9}$$

结合$(8)(9)$，就非常像$(5)$​了。

和$(6)$一样，WKV算子也可以写成RNN的形式，这个时候$w$的设计就非常巧妙了：

$$\begin{aligned} a_0,b_0 &= 0 \\ a_t &= e^{-w} \odot a_{t-1} + e^{k_t} \odot v_t \\ b_t &= e^{-w} \odot b_{t-1} + e^{k_t} \\ \operatorname{wkv}_t&= \frac {a_{t-1} + e^{u+k_t} \odot v_t} {b_{t-1} + e^{u+k_t}} \end{aligned} \tag{10}$$

同样，状态包括分子和分母，分别是$a,b$。前一步的状态要乘$e^{-w}$，再加上key与value计算出来的结果。由于$(8)$中定义了$w$的形式是相对距离个$e^{-w}$相乘，所以这里每一步都是乘$e^{-w}$。到了最后一步输出，也是一个作为分子，一个作为分母，当前时刻额外的是用$u$。

⚠️在实际计算中，$(10)$中的指数计算可能面临上溢风险，所以计算的时候会额外使用一个$p_t$来保存$a_t,b_t$中共享的幂。（具体原理可以看论文附录D）。本来$\operatorname{wkv}$的参数量是$4DL$的，但是由于计算问题会变成$5DL$。

RWKV的$(8)$和$(10)$带来了time-parallel mode和time-sequential mode两种模式，分别用在训练和推理中。

训练时处理打包成batch的数据，RWKV拥有$\mathcal{O}(BTd^2)$的时间复杂度，并且可以并行计算。

Channel-Mixing

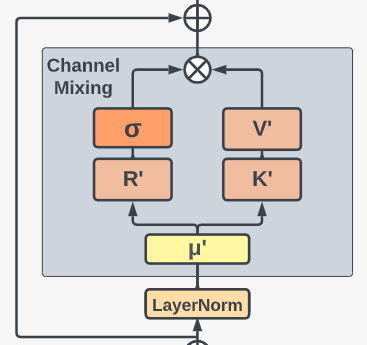
channel-mixing也会进行Token shift：

$$\begin{aligned} r^\prime_t &= W^\prime_r \cdot (\mu^\prime_r \odot x_t + (1-\mu^\prime_r) \odot x_{t-1}) \\ k^\prime_t &= W^\prime_k \cdot (\mu^\prime_k \odot x_t + (1-\mu^\prime_k) \odot x_{t-1}) \\ o^\prime_t &= \sigma(r^\prime_t) \odot (W^\prime_v \cdot \sigma_{ReLU^2}(k^\prime_t)) \end{aligned} \tag{11}$$

其中，$\sigma_{ReLU^2}$表示ReLU激活后再平方，论文没说动机。

假如把Token shift去掉，上图左侧一路相当于一种channel attention，右侧则像Transformer中的两层FC构成的FFN。

实验

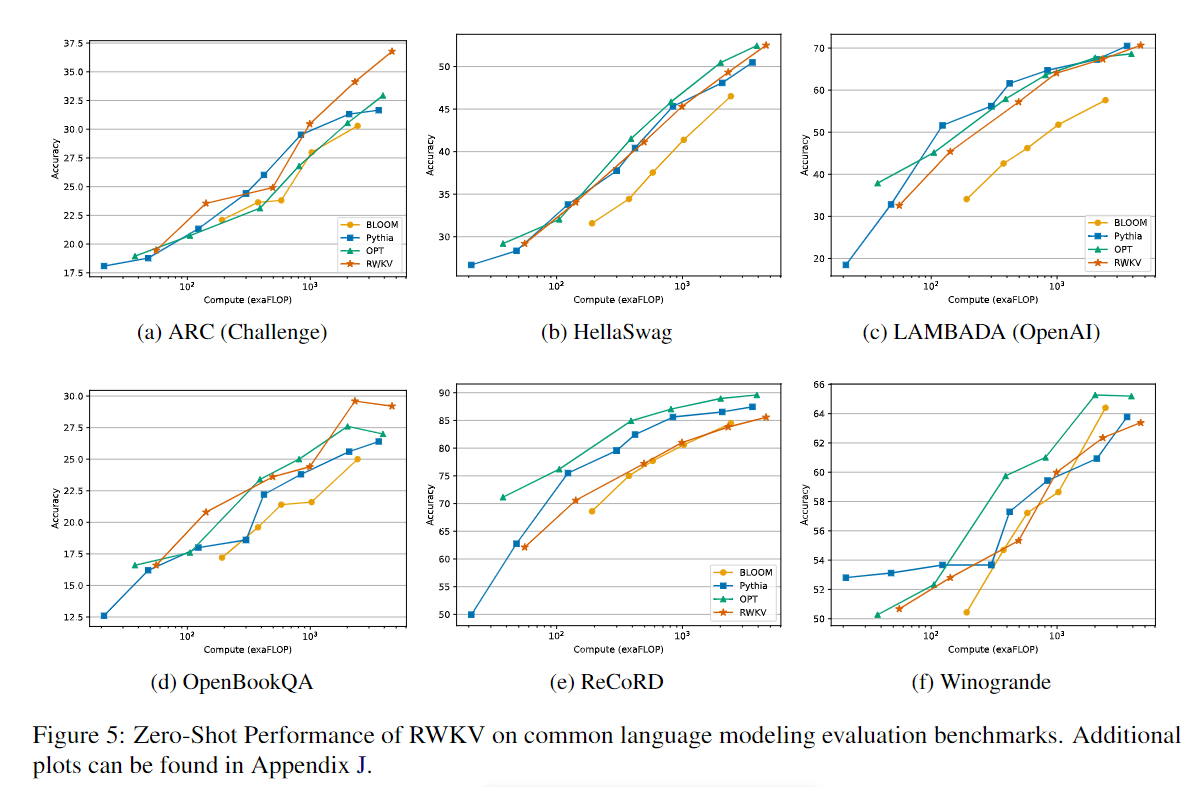
☝️ 不是很懂NLP的评测标注，Fig 5中表现其实一般，但是已经比较有竞争力了。

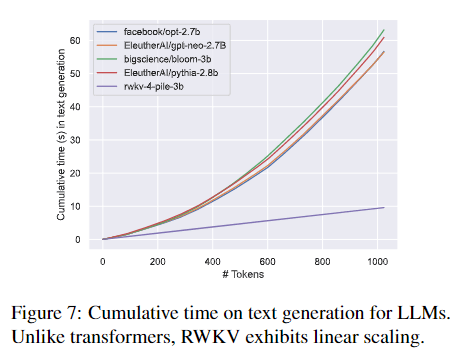
☝️RWKV最有优势的地方就算节省资源，在token数量很大时，仍然保持较快的处理速度。

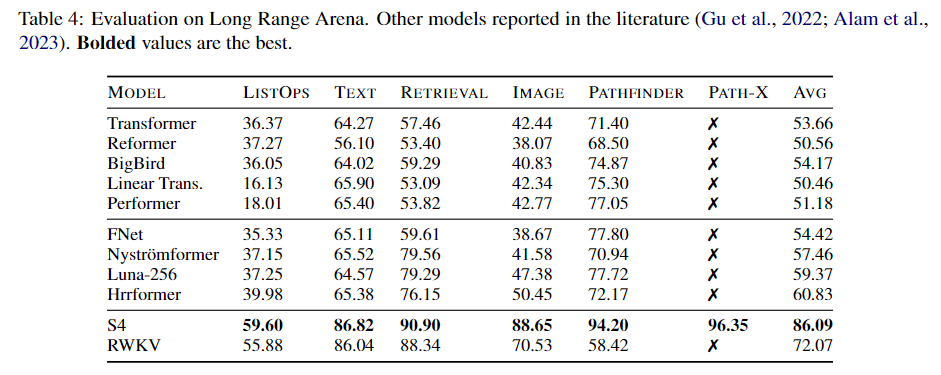
☝️同时，在Long Range的评价标准下，RWKV获得了除开S4外基本最优的性能，但是S4超了很多，

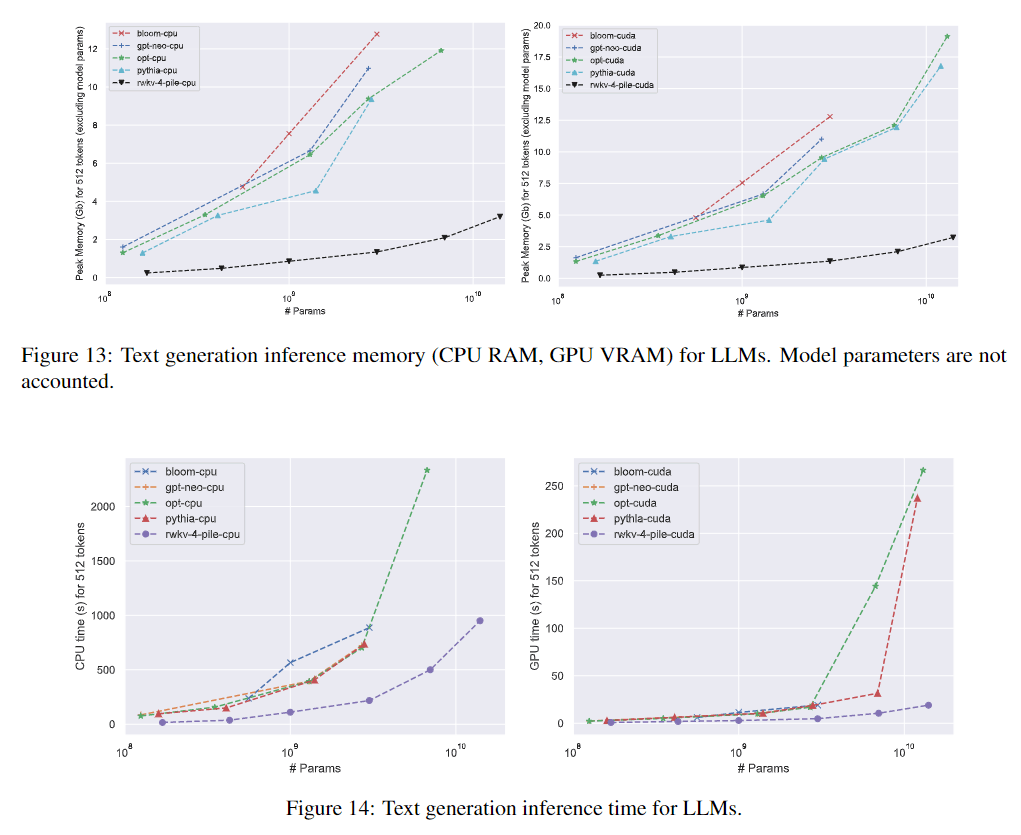
☝️ 在不同参数量模型的推理速度上，RWKV具有非常非常明显的优势。

结论

RWKV展示了线性Transformer的另一种可能，并花费巨大成本，积极在LLM赛道上进行实验。

RWKV目前的不足，作者自己分析是在其相较于Transformer的建模能力的天生差距，此外还有就是RWKV的recurrent的特性也使得其对prompt的要求非常高，prompt的顺序都会影响巨大。

RWKV未来野心勃勃，计划涉及多模态等领域，并提到了其替换cross-attention的目标，但是没说具体怎么做。

1. Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention ↩
2. Transformer Dissection: A Unified Understanding of Transformer’s Attention via the Lens of Kernel ↩
3. Asymmetric Kernel Learning ↩