本文最后更新于:2024年2月23日 中午
学习笔记 Beta分布与狄利克雷分布
在调研Evidential Deep Learning(EDL)的时候了解到EDL是基于Dirichlet分布的,由于这方面数学知识不够,所以额外调查了关于Beta分布、Dirichlet分布的知识,汇总为本学习笔记。
总的来说,Beta分布和Dirichlet分布都是一种“分布的分布”(a distribution on probability distribution)。
Beta分布
棒球的例子
在棒球运动中,运动员的击球率常常作为一个评价标准,击球率的定义是:击中的球数除以击球的总数。现在有一个新运动员小明,我们希望对小明的击球率做一个估计,但是小明在比赛中只打了一个球,并且击中了,直接计算击球率就是100%。显然,这是不合理的,但是应该怎么进行估计呢?
对于这个问题,我们可以使用beta分布来进行建模。根据统计,0.266是正常水平的击球率,大部分选手的击球率在0.215到0.360之间。下图是对Beta分布的两个参数分别取81和219的概率密度函数(PDF),其均值为0.27,分布主要落在[0.2,0.35],符合棒球运动中的统计规律。
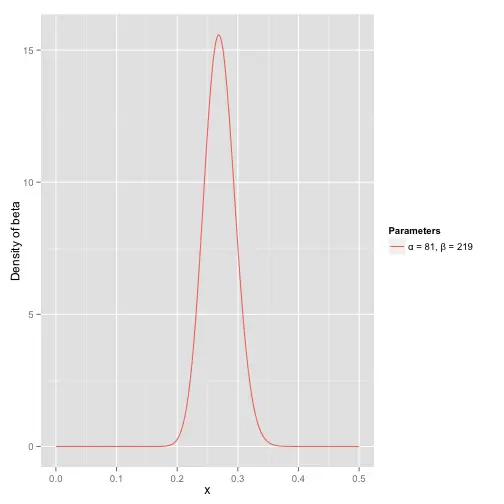
估计小明的击球率的方法就是Beta(α+hits,β+misses),即令α加上击中次数、β加上未击中次数,结果能得到下面这个图:
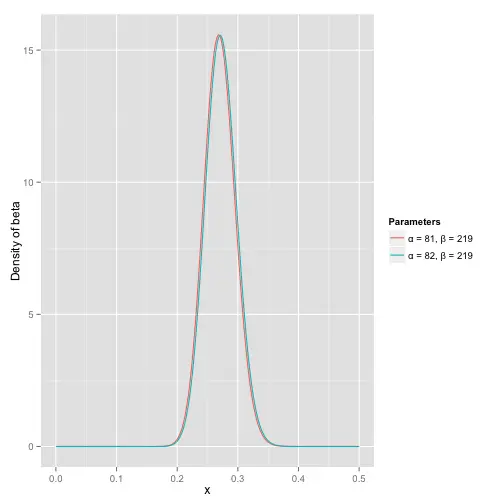
这里可以看到,小明击球率很可能在0.27左右,显然是一个比100%更合理的数字。但是很遗憾的是,和棒球运动整体统计的曲线没什么变化,因为击中一次实在是太少了,但是随着小明继续击球,我们会得到新的曲线:
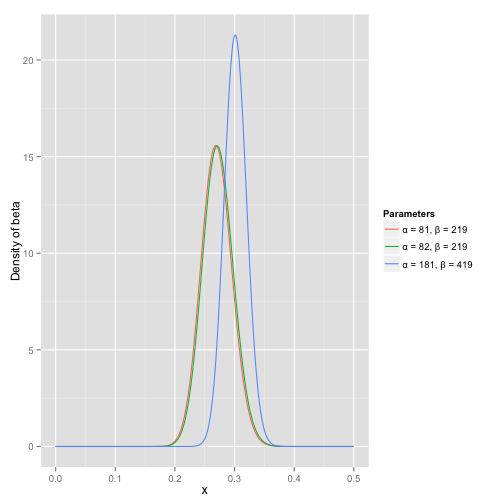
此时,直接估计的击球率是100+200100=0.333,但是根据beta分布的均值则是α+βα=181+419181=0.302(如何求均值后面再说,这里只说结论)。这里的不一样是因为,我们设置的初始的α=81,β=219的参数表示我们给予了“小明在击球前已经成功81次、失败219次”的先验信息。
整体来看,小明的击球应该服从一个参数为θ的二项分布,而这里的beta分布是一个能够帮助我们建模θ的分布,所以beta分布是一种“分布的分布”。当你不知道一个东西的具体概率是多少时,beta分布能给出所有概率出现的可能性的大小。
公式推导
Beta的PDF
根据二项分布,小明总共击n个球,击中x个的概率是p(x)=\pmatrix{n \\ x} \theta^x(1-\theta)^{n-x},这里θ就是击球的概率,我们以其为变量,将刚才的式子表示为θ的参数:
f(θ)∝θa(1−θ)b=k⋅θa(1−θ)b
其中,a,b是常数,表示成功(击中)和失败(未击中)的次数,θ是[0,1]范围内的概率。为了f(θ)是概率,需要乘一个k来标准化,这个k就是:
k=∫01θa(1−θ)bdθ1
即除以θa(1−θ)b曲线下的面积。
令α=a+1,β=b+1,则Beta分布的PDF为
f(θ;α,β)=∫01θα−1(1−θ)β−1dθθα−1(1−θ)β−1=B(α,β)θα−1(1−θ)β−1
回到第一个式子,我们可以发现其实\pmatrix{n \\ x}=C^x_n=\frac{n!}{x!(n-x)!},所以B(α,β)=(α+β−2)!(α−1)!(β−1)!,而Γ(gamma)函数是阶乘的推广,所以Beta的PDF还可以表示为:
f(θ;α,β)=Γ(α)Γ(β)Γ(α+β)θα−1(1−θ)β−1
其中,Γ函数函数为:
Γ(z)=∫0∞tz−1e−tdt=(z−1)!
Beta的统计性质
-
期望
E(X)=∫01xf(x;α,β)dx=∫01xB(α,β)xα−1(1−x)β−1dx=B(α,β)1∫01xα(1−x)β−1dx=B(α,β)B(α+1,β)=Γ(α)Γ(β)Γ(α+β)⋅Γ(α+β+1)Γ(α+1)Γ(β)=α+βα
最后一步根据阶乘的思路化简即可
-
二阶矩
E(X2)=∫01x2f(x;α,β)dx=∫01x2B(α,β)xα−1(1−x)β−1dx=B(α,β)1∫01xα+1(1−x)β−1dx=B(α,β)B(α+2,β)=(α+β)(α+β+1)α(α+1)
-
方差
D(X)=E(X2)−E2(X)=(α+β)2(α+β+1)αβ
根据贝叶斯估计求θ的分布
根据贝叶斯公式,有:
P(θ;data)=P(data)P(data;θ)P(θ)∝P(data;θ)P(θ)
因为数据的分布是一个定值,所以忽略它,只保留分子,即先验分布与参数为θ的二项分布乘积。
P(θ;data)P(θ;data)∝θx(1−θ)(n−x)⋅θα−1(1−θ)β−1∝θα+x−1(1−θ)(β+(n−x)−1)=B(α′,β′)θα′−1(1−θ)(β′−1),where α′=α+xdata中成功次数,β′=β+(n−x)data中失败次数
所以根据数据和先验对参数的估计方法,就是先验的α加上成功次数、先验的β加上失败次数。
红鞋蓝鞋的例子
假如观察小明每天会穿一双蓝色的鞋子或者一双红色的鞋子来到学校,但是我们对他穿什么颜色的鞋子没有任何先验知识,那么应该怎么利用beta分布进行估计呢?
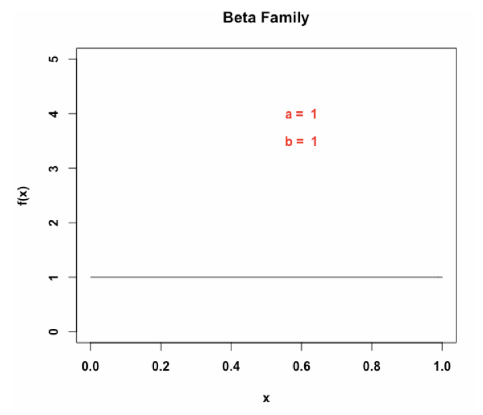
答案是将先验设置为平均分布,如上图所示,将α和β都设置为1即可获得一个均匀分布的beta分布,然后我们再根据观察往α和β上加蓝鞋红鞋的天数。
Dirichlet分布
然而,Beta分布只能对成功/失败进行建模,假如小明穿红绿蓝三种颜色的鞋子时,beta分布就无能为力了,所以,狄利克雷分布就出现了。
Dirichlet分布是Beta分布的拓展,Beta分布是Dirichlet分布的特例。
Beta分布的公式为:
f(θ)=Γ(α)Γ(β)Γ(α+β)θα−1(1−θ)β−1
而Dirichlet分布的公式为:
f(θ)=∏kΓ(αk)Γ(∑kαk)k=1∏mθkαk−1
其中总共有m个参数,αk是其参数,同样也可以写作:
f(θ)=B(α)1k=1∏mθkαk−1
统计性质
参考文献
狄利克雷分布(Dirichlet Distribution) - 知乎 (zhihu.com)
来源:如何通俗理解 beta 分布? - 小杰的回答 - 知乎
【统计学进阶知识(一)】深入理解Beta分布:从定义到公式推导 - 知乎 (zhihu.com)
狄利克雷分布 - 维基百科,自由的百科全书 (wikipedia.org)
Β分布 - 维基百科,自由的百科全书 (wikipedia.org)
Intro to 狄利克雷(Dirichlet)分布 - 知乎 (zhihu.com)



