综述笔记 A Comprehensive Survey on Test-Time Adaptation under Distribution Shifts

论文链接：A Comprehensive Survey on Test-Time Adaptation under Distribution Shifts (arxiv.org)

综述配套repo：tim-learn/awesome-test-time-adaptation: Collection of awesome test-time (domain/batch/instance) adaptation methods (github.com)

中科院院士谭铁牛23年3月在Arxiv上的关于Test-Time Adaptation的一篇综述，笔者对此领域不了解，所以此笔记仅涉及此综述的大致内容，并且叙述顺序与论文不一定平行。

什么是Test-Time Adaptation？

首先，虽然Test-Time Adaptation可以缩写为TTA，但是一般说的TTA是Test-Time Augmentation（测试时增强）而非Test-Time Adaptation（测试时适应），在文中2.6介绍了两者的关系，即TT-Adapt会考虑训练与测试的分布偏移，而TT-Aug是一种测试时通过数据增强来提升性能、估计可信度的方式，本文的TT-Adapt可以利用TT-Aug，但是讨论范围更广。本笔记接下来将Test-Time Adaptation缩写为TTA。

TTA是一种迁移学习和域适应的特例，其关注将一个在source domain的预训练模型在进行预测前，适配到一个没有标签的target domain中。如下图所示，TTA只有预训练模型和测试数据（没有训练数据）。例如，一个模型在猫狗的正面照片数据集中训练好了二分类任务，然后测试数据是猫狗的背面照片数据集，或者是猫狗猪鸡鸭的照片数据集。

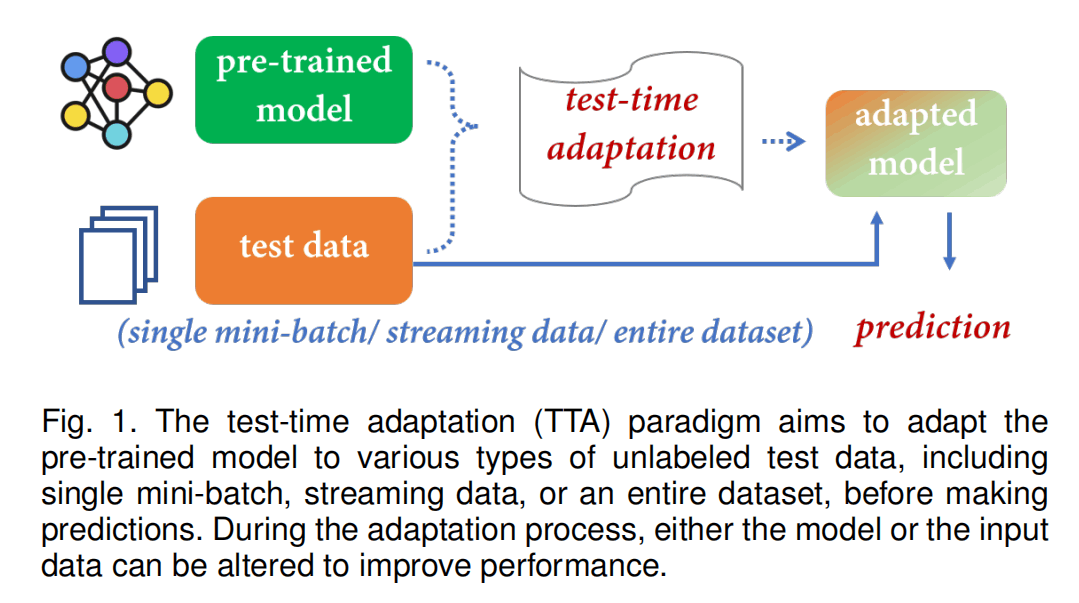
TTA可以分为test-time domain adaptation（又称source-free domain adaptation，SFDA）、test-time batch adaptation（TTBA）、online test-time adaptation（OTTA）三类。

• SFDA：使用整个测试集进行适配（将测试集看作没有标签的训练集进行多轮训练）
• TTBA：仅使用一个batch的测试集进行适配（一次只能涉及到一个batch的信息，不同batch之间是独立的，batch size可以为1）
• OTTA：使用整个测试集，但是是以一种online的形式（一个一个batch来，模型可以利用先到的batch的知识为后面的batch做推理）

此外，文章还调研了TTA中出现的标签偏移（test-time prior adaptation，TTPA）情况：

• TTPA：训练和测试的标签分布$p(y)$不同，但是$p(x|y)$不变（猫狗二分类时，突然地球上的猫猫数量变成了原来的100000倍，此时$p(y_{猫})$大了许多，但是对于某张猫的照片($x$)来说，是猫的概率和是狗的概率不变）

这里有几个近似的概念：

• 概念漂移（Concept shift/drift）：$p(y|x)$变化，但$p(x)$不变。比如一个男人女人照片二分类的模型，随着社会的进步，我们将一部分心理女性的男人认为是女人。此时，照片的分布是不变的，但是我们对性别标签的定义发生了变化。
• 标签漂移（Label/prior shift/drift）：$p(y)$变化，但$p(x|y)$不变。比如猫、豹、虎三分类的模型，训练的时候使用的是$1:1:1$的数据，但是测试时大多数人都拍猫猫而不是豹子或者老虎的照片来输入模型，此时标签发生了变化，假如模型对猫猫的分类能力更弱，那么模型在测试时的性能就会降低，但是猫豹虎被拍的照片还是差不多那样，分布没有变化（猫猫照片中可能有一只手在撸，但是豹虎照片基本都是长焦拍摄）。
• 特征漂移（Feature/Covariate shift/drift）：$p(x)$变化，但$p(y|x)$​不变。这个应该是最经常考虑的情况了，比如用猫狗的真实照片训练了二分类模型，但是用户用手绘的图像去分类，那模型性能就会受到影响。

说了这么多，其实这个不是重点。

Source-Free Domain Adaptation（SFDA）

对于一个在Source域$\mathcal{D}_S$上训练好的分类器$f_S:\mathcal{X}_S \rightarrow \mathcal{Y}_S$，SFDA旨在利用$f_S$的知识来推理Target域$\mathcal{D}_{\mathcal{T}}$上的样本，其中$\mathcal{D}_{\mathcal{T}}$的所有数据在adaptation中都会被用到。

就是在没有标签的测试集上相办法再训一下。

SFDA有伪标签（Pseudo-labeling）、一致性训练（Consistency Training）、基于聚类的训练、Source分布估计、自监督学习的方法。

1. 伪标签

   从半监督学习中来的，为没有标签的数据打上一些伪标签再进行训练。这类方法致力于提升伪标签的可信度或者进行更鲁棒的利用。

2. 一致性训练

   也是从半监督学习来的，基于机器学习的manifold假设

   高维数据实际以低维manifold结构嵌入在高维空间中，比如下图中数据点的分布，要衡量两个点的距离，直接三维空间的欧几里得距离不合适，红线这种绕弯才是在这个流体上的最近路线。在机器学习中，比如人脸的64x64图像，分布在一个$64\times64$维的空间中，但是在这个空间随机采样出来的根本不是人脸，大多数都是噪声，人脸的图像可能只分布在一个manifold上，有冗余、能压缩，所以机器学习可以获得其低维度的“特征”。

   假设男人的图像在A点，女人的图像在B点，那么$(A+B)/2$的点就是两个人融合的中性的人的图像，而不是一堆噪声。

   

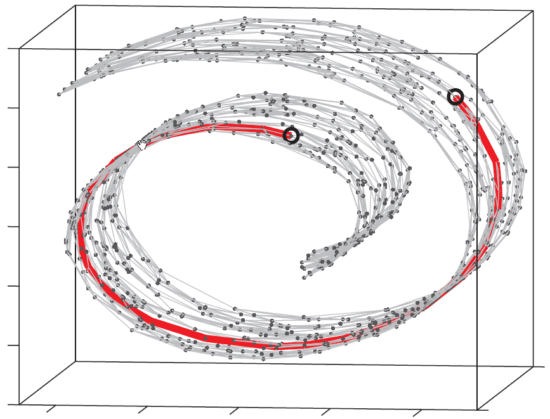
   求简要介绍一下流形学习的基本思想？ - 麋路的回答 - 知乎

   总之，一致性训练的方法旨在数据空间或者参数空间发生变化时，也有一致性的输出。比如照片光照发生变化，或者照片旋转，不会改变这个照片是猫猫🐱的照片的事实。

3. 基于聚类的训练

   也是从半监督学习力来的思想，认为分类时特征符合聚类假设，即决策边界存在于低密度的区域。基于聚类的SFDA方法致力于减少网络预测的不确定性或者鼓励目标域特征聚类。

4. Source域分布估计

   这个方法通过从预训练模型中估计其训练数据，将SFDA转换为一个域适应（Domain Adaptation）问题，而域适应问题已经被广泛研究过了。

   Domain Adaptation（DA）就是有带标签的源域数据和不带标签的目标域数据，需要得到一个在目标域上表现好的模型。

5. 自监督学习

   自监督学习可以通过构建任务来从无标签的数据中学习知识。所以直接用自监督方法在测试集上训就可以了。

与平常迁移学习的范式不同，SFDA通常只更新特征编码器的参数，冻结分类器的参数。比如我们通常使用ImageNet上1000分类预训练的ResNet，会保留其backbone，替换其classifier。而SFDA是为了让编码器适应目标域的分布，所以会反过来微调backbone而冻结classifier。但是，具体调整哪一部分参数是不一定的，有的调节BatchNorm、有的调节卷积和FC……而对于基于Source域分布估计的模型，它们只训练source->target的映射器。

虽然大部分SFDA都使用原本的预训练模型，但是也有方法对原来的模型就进行修改，这篇综述在3.2.7进行了讨论。

此外，3.3还讨论了SFDA的各种变种场景。

Test-Time Batch Adaptation（TTBA）

TTBA可以看作是SFDA的特例，即测试集大小=batch size。而当batch size=1时的特例又可以叫做Test-Time Instance Adaptation。但是这里主要还是讨论泛化一点的TTBA：

对于一个在Source域$\mathcal{D}_S$上训练好的分类器$f_S$，以及一个batch的无标签的目标域$\mathcal{D}_{\mathcal{T}}$的instance$\{x^1_t,x^2_t,\cdots,x^B_t\}$，TTBA旨在利用利用$f_S$的知识来推理batch中的样本。其中，对每个instance是不独立的，batch中的其它数据会造成影响。

TTBA有基于BatchNorm矫正（BatchNorm Calibration）、模型优化、元学习（Meta-Learning）、输入适应、动态推理的方法：

1. BatchNorm Calibration

   BatchNorm公式如下，其中$\mathbb{E}[X_S],\mathbb{V}[X_S]$通过指数滑动平均更新，而$\gamma,\beta$通过梯度下降法更新。在测试的时候，训练时的统计量会保存下来。

   $$\hat{x}_s=\gamma \cdot \frac{x_s-\mathbb{E}[X_S]}{\sqrt{\mathbb{V}[X_S]+\epsilon}}+\beta$$

   但是一篇文献（AdaBN）认为BN层的统计特征蕴含了领域相关的知识，可以通过将旧的统计特征更新为目标域的统计特征来进行适配。这种方法对于Batch size小时有估计不准的问题，但是4.2.1中提到了一些文献来解决这些问题。

2. 模型优化

   这类方法需要调节预训练模型的参数，分为（1）训练阶段引入无监督的辅助任务，测试时利用此辅助任务微调。（2）测试时使用新的任务避免训练引入新的loss。

3. 元学习

   元学习能够通过非常少的样本和梯度下降部署进行迁移适配，分为反向传播和前向传播两种，后者不改变参数。

4. 输入适应

   与第2点的优化模型不同，这类方法改变输入进去的数据。文中说这个和prompt tuning类似，通过无监督的方法对输入进行改变。

5. 动态推理

   这类方法涉及到多个模型，其通过学习组合多个模型的权重来进行适配。

Online Test-Time Adaptation（OTTA）

对于实际使用时，数据可能是以online的形式送进来的，所以OTTA对于一个在Source域$\mathcal{D}_S$上训练好的分类器$f_S$，以及一系列的无标签的目标域$\mathcal{D}_{\mathcal{T}}$的batch$\{B^1_t,B^2_t,\cdots\}$，旨在利用$f_S$的知识来在线推理测试集中的样本，其可以利用之间见过的batch的知识。

这类方法相较于TTBA来说利用的数据更多了，相较于SFDA更符合现实情况，但是容易造成错误的累积以及灾难性遗忘的问题。具体有基于BatchNorm Calibration、熵最小化、伪标签、Consistency Regularization的方法：

1. BatchNorm Calibration

   和TTBA的差不多，只不过是可以继续多个batch的batch norm统计。

2. Entropy Minimization

   文中没有概括这个方法的流程，之说了是处理无标签数据常用的方法。

3. Pseudo-labeling

   与SFDA的伪标签类似，一边利用伪标签学习，一边标记下一个batch的伪标签。

4. Consistency Regularization

   感觉与SFDA的一致性训练类似。

为了避免灾难性遗忘，一些方法会使用训练集的一小部分数据插入到测试集，再使用以上的方法训练。还有的方法会减少改变的参数。

OTTA对于输入batch的建模一般是假设平稳的，但是有的方法假设不断送进来的batch的分布会变化。

Test-Time Prior Adaptation（TTPA）

对于一个在Source域$\mathcal{D}_S$上训练好的分类器$f_S$，以及无标签的目标域$\mathcal{D}_{\mathcal{T}}$，TTPA旨在测试集出现prior shift时矫正$f_S$的预测$p_{\mathcal{S}}(y|x)=f_{\mathcal{S}}(x)$​。

prior根据贝叶斯公式可以有以下等式：

$$\begin{aligned} & p_{\mathcal{T}}(y | x)=\frac{p_{\mathcal{T}}(x | y) p_{\mathcal{T}}(y)}{p_{\mathcal{T}}(x)}=p_{\mathcal{S}}(x | y) \cdot \frac{p_{\mathcal{T}}(y)}{p_{\mathcal{T}}(x)} \\ & \quad=\frac{p_{\mathcal{S}}(y | x) p_{\mathcal{S}}(x)}{p_{\mathcal{S}}(y)} \cdot \frac{p_{\mathcal{T}}(y)}{p_{\mathcal{T}}(x)} \propto p_{\mathcal{S}}(y | x) \cdot \frac{p_{\mathcal{T}}(y)}{p_{\mathcal{S}}(y)}\end{aligned}$$

$p_{\mathcal{T}}(y | x)$是矫正过后的概率，其相当于矫正前的概率$p_{\mathcal{S}}(y | x)$乘上一个标签偏移的系数$\frac{p_{\mathcal{T}}(y)}{p_{\mathcal{S}}(y)}$​，所以关键在于如何估计这个系数。方法包含基于混淆矩阵的、基于最大似然估计的以及两者结合的。

1. 混淆矩阵

   令$\left[C_{\hat{y} \mid y}\right]_{i, j}$为混淆矩阵，有下式：

   $$p_{\mathcal{T}}(\hat{y}=i)=\sum_{j=1}^C\left[C_{\hat{y} \mid y}\right]_{i, j} p_{\mathcal{T}}(y=j), i=1, \ldots, C$$

   即模型在target的预测的概率等于其实际标签与混淆矩阵的乘积（就是 预测是某类别的概率=正确概率+本来是其他类但是预测错成这个类的概率）。反过来的话，对混淆矩阵求逆，即$\hat{p}_{\mathcal{T}}(y) = [C]^{-1} p_{\mathcal{T}}(\hat{y})$，可以通过预测概率分布得到真实的概率分布$p_{\mathcal{T}}(y)$，而混淆矩阵可以通过验证集得到，根据理论混淆矩阵在prior shift的情况下不改变。

   此外，6.2.1讨论了一些方法利用混淆矩阵估计分布。

2. 最大似然估计

   嗯，没看懂😵

3. 混淆矩阵与最大似然估计结合

   也没看懂捏😵

总结

TTA的情景是预训练数据未知、预训练模型已知、无标签测试集已知，从某个角度看，TTA也是为了提升模型泛化能力。综述的最后提到了几个热门方向：

1. 首先是在更多的下游任务中使用TTA，之前的TTA一般都是图像分类
2. 其次是用在black-box的预训练模型上，假如只能获得模型预测概率分布或者离散的预测结果，如何进行适配呢？比如你买了某家公司的LLM的api。
3. 目前的TTA对于test-time的假设大多只是分布不一样，而很多情况下目标域的标签类别就可能不一样，属于open-set的问题。
4. 对于大模型来说，适配的成本也要考虑，所以Memory-efficient的方法也是新方向。
5. TTA的方法使用的是一个静态的预训练模型，但是假如这个预训练模型在实际中需要更新呢？

在监控视频异常检测领域可能比较适用OTTA的方法，假如训练好一个模型，部署在一个摄像头之后，摄像头就会源源不断提供视频流，假如能够根据部署的实际场景来对模型进行一些适配与优化就很好了。但是这种场景下更需要的还是open-set的方法，并且这种场景有非常严重的标签不均衡。