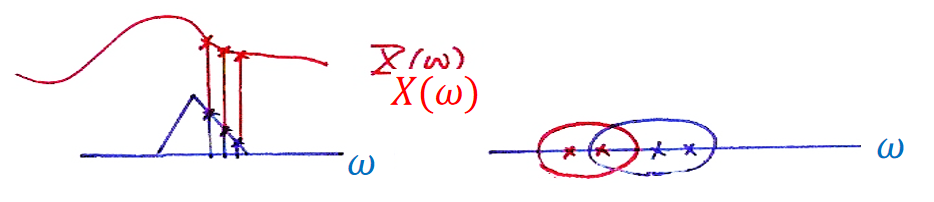本文最后更新于:2022年7月21日 下午
语音信号处理#2 频域分析:傅里叶频谱、语谱图、倒谱、MFCC(附代码)
为什么要进行频域分析?因为人耳是根据频率来听声音的,如下图,耳蜗的各个部分可以分析出不同频率的信号。

如何获取频谱
信号的频域都是使用快速傅里叶变换(Fast Fourier Transform, FFT)来获得的,为了获得良好的频域信号,需要先进行三个步骤:预加重(pre-emphasis)、端点检测(endpoint detection)、分帧加窗(enframe, windowing)。
-
预加重
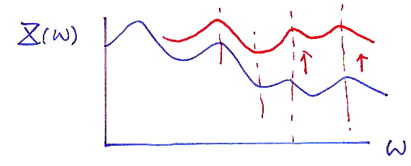
如下图,假如不进行预加重,那高频的信号会越来越低(如蓝线),所以我们要对高频信号提前施加权重,使用公式x(n)=x(n)−ax(n−1),其中0<<a<1,一般取0.98等较大的值。
公式表示在z域就是H(z)=1−az−1。
-
端点检测
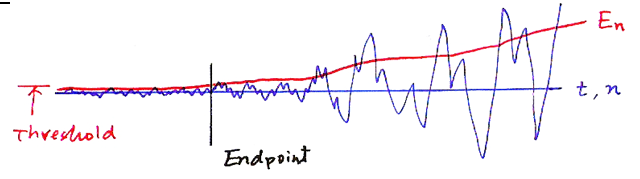
一段语音中人不可能一直在说话,而是有停顿,所以我们要检测停顿以免干扰信号。简单的可以用短时能量来检测,比如sh这个发音(“是”发音的前面)很像噪声,但是计算出来的能量不一样。人发音的时候能量更大,而噪声的能量更小,需要设定一个阈值就能分开。这个阈值可以通过噪声样本得到,即让人先沉默一段时间,然后这段时间的E作为阈值。
-
分帧加窗
上一节说过啦,就不再说了
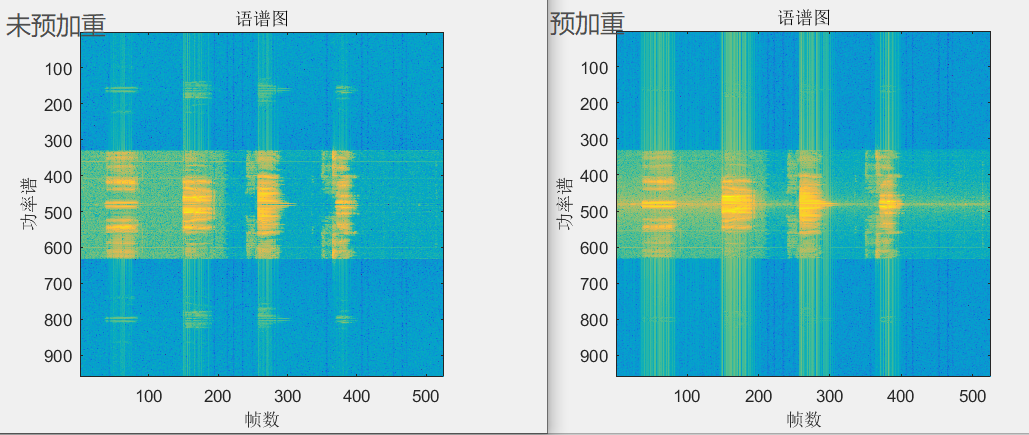
进行完上面这些预处理之后,就可以直接FFT到频域啦。语音信号可以被可视化为语谱图,横轴表示时间,纵轴表示频率,颜色表示频率的对应的值。要注意的是可能需要对语谱图10log10更能看清,并且为了让0频率在中间,可以用fftshift挪过去。
MATLAB实现
可以看到预加重了的信号高频更绿,也就是把高频提升了起来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| clear all
close all
clc
input_audio = 'yiersansi.m4a';
[x,Fs] = audioread(input_audio);
x = x(2:end,1) - 0.98 * x(1:end-1,1);
[len,~] = size(x);
frame_second = 20;
overlap_percent = 0.5;
frame_size = floor(Fs * 0.001 * frame_second);
overlap = floor(overlap_percent * frame_size);
for n = 1:(frame_size-overlap):len-frame_size
num = (n-1) / (frame_size-overlap) + 1;
y(:,num) = x(n:n+frame_size-1);
end
[d,frame_num] = size(y);
w = hamming(d);
for n = 1:frame_num
y_hat(:,n) = abs(fftshift(fft(y(:,n) .* w))) .^ 2;
end
figure(1);subplot(121);plot(x);
subplot(122);imagesc(10*log10(y_hat)); title('语谱图');xlabel('帧数'); ylabel('功率谱');
|
倒谱(Cepstrum)
倒谱来源于语音信号的建模:语音信号z(t)可以看作是声门激励信号x(t)和声道冲激响应y(t)的卷积:z(t)=x(t)∗y(t)。声门是声带之间的区域,声门每开启和关闭一次的时间叫做基音周期,声道是从声门到嘴唇的通道,由咽、鼻、口构成,其中口腔是最重要的部分。也就是说,人发出的语音就是声道冲激响应随着声门一次次发出的信号。
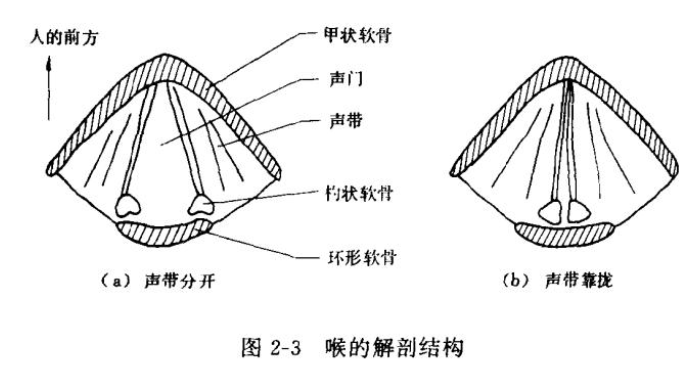
声门激励信号x(t):发清音时(声带不振动,如拼音b p),为能量较小的白噪声;发浊音时(声带振动,如拼音m n),为以基音周期为周期的冲激序列。
声道冲激响应y(t):是一个双边衰减序列。
基音周期:据统计,人的基音周期Tp范围为[2.5,20]ms,也就是[50,400]Hz。假如采样频率是10kHz,那么计算下来基音周期就是[25,200]个点。对应关系是2.5ms=400Hz=25 point。
因为这两个信号是卷积在一起的,为了把这两个分开,我们要解卷积,可以使用同态处理方法,将卷积变成相加。
同态处理
同态处理指的是将非线性组合信号通过某种变换转换成线性组合信号,然后通过线性操作进行处理的方式。
-
z(t)=x(t)y(t)
这种相乘的非线性组合信号正常来说很难分开,可以先进行log运算转换成logz(t)=logx(t)+logy(t)。然后DFT到频域进行处理,然后再IDFT回来再进行个指数运算就能转换回来,是图像中的同态滤波。
-
z(t)=x(t)∗y(t)
时域卷积转到频域就是相乘Z(w)=X(w)Y(w),然后和上面这种情况一样logZ(w)=logX(w)+logY(w),再转回时域进行线性处理。
下图(b)是卷积同态系统,先经过特征系统,再线性处理,最后逆特征系统。特征系统就是一个Z变换 -> log/e -> 逆Z变换的过程。
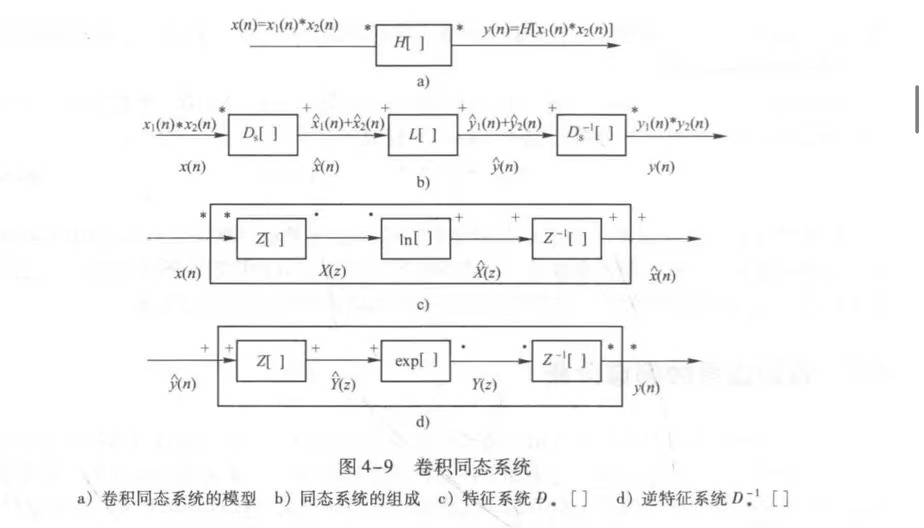
计算倒谱与复倒谱
倒谱(Cepstrum)的英文就是频谱(Spectrum)前四个字母倒过来。
- z(t)的复倒谱z^(t)就是进行Z变换后取对数然后再逆Z变换的结果,这个过程也叫做特征系统D∗[⋅]。
- z(t)的倒谱z^(t)也差不多,就是在Z变换之后会取幅值,因为一般不注重相位信息。
实际中不用Z变换,直接FFT。
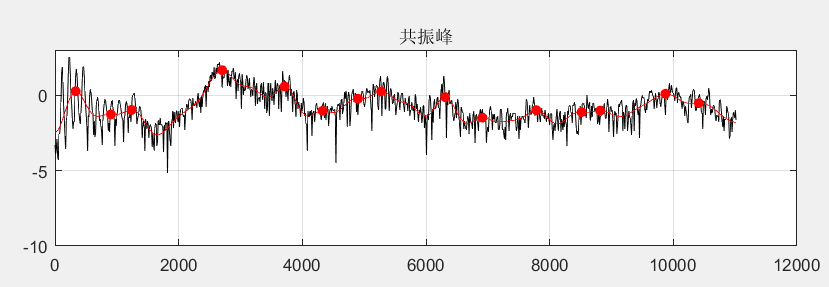
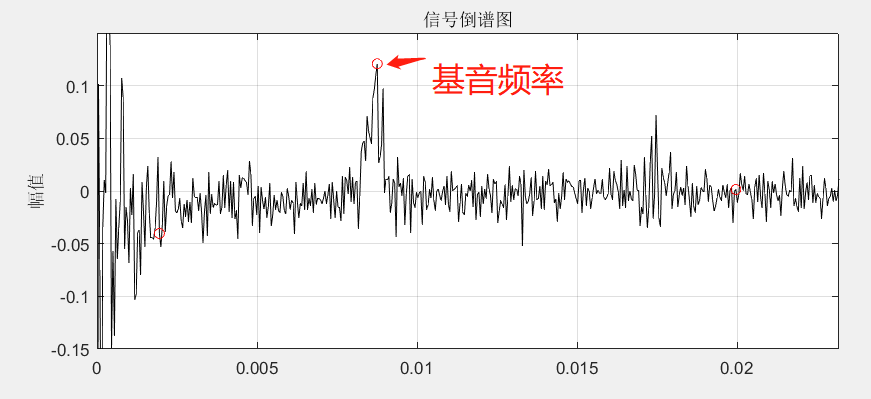
利用倒谱求共振峰和基音频率
共振峰就是频谱的包络,基音频率就是倒谱的一个峰值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
clear all; clc; close all;
input_audio = 'F716.wav';
[yy,fs] = audioread(input_audio);
start = 2500;
nfft = 2048;
time = (0:nfft-1)/fs;
yy = yy(2:end,1) - 0.98 * yy(1:end-1,1);
y = yy(start:start-1+nfft,:) .* hanning(nfft);
figure(1), subplot 211; plot(time,y,'k');
title('信号波形'); ylabel('幅值'); xlabel(['时间/s']); grid;
Y=log(abs(fft(y)));
nn=1:nfft/2; ff=(nn-1)*fs/nfft;
figure(2); subplot 311; plot(ff,Y(nn),'k');
grid on; hold on;
z=ifft(Y);
figure(1),subplot 212; plot(time,z,'k'); hold on;
axis([0 time(512) -0.15 0.15]); grid;
ylabel('幅值'); title('信号倒谱图');
mcep=floor(fs / 500);
zy=z(1:mcep+1);
zy=[zy' zeros(1,nfft-2*mcep-1) zy(end:-1:2)'];
ZY=fft(zy);
figure(2); subplot 312;
plot(ff,real(ZY(nn)), 'k'); grid;
title('声道冲激响频谱'); ylabel('幅值'); xlabel(['频率/Hz']);
ft=[zeros(1,mcep+1) z(mcep+2:end-mcep)' zeros(1,mcep)];
FT=fft(ft);
figure(2)
subplot 313; plot(ff,abs(FT(nn)),'k'); grid;
title('声门激励脉冲频谱')
ylabel('幅值'); xlabel(['频率/Hz']);
figure(2), subplot 311;hold on;
plot(ff, real(ZY(nn)), 'red'); hold on;
[pks, locs] = findpeaks(real(ZY(nn)));
scatter(ff(locs), pks, 'red', 'filled');
axis([0 12000 -10 3]);
grid on;
hold off;
title('共振峰');
st_point = floor(fs / 500);
end_point = floor(fs / 50);
loc = find(max(z(st_point:end_point)) == z(st_point:end_point)) + st_point - 1;
pitch_freq = 1 / time(loc)
figure(1);subplot 212;
scatter(time([loc, st_point, end_point]), z([loc, st_point, end_point]), 'red');
|
MFCC
MFCC是Mel Frequency Cepstrum Coefficient梅尔频率倒谱系数的缩写,是语音识别领域常用的一种特征提取方式。
MFCC同样也是模拟人的耳蜗,耳蜗不同的地方听到的是不同的频率,但是之间仍然有交叉重叠,并不是说这边听40~50Hz,另外一边听50~60Hz。所以MFCC使用三角滤波,对某个频率周围进行加权(类似计算机视觉里常用的高斯平滑)。还有一个问题,就是耳蜗听频率并不是均匀分布的,而是越高频越稀疏,所以MFCC使用不同宽度的三角波,越高频越宽,这叫做Mel-scale滤波器组。
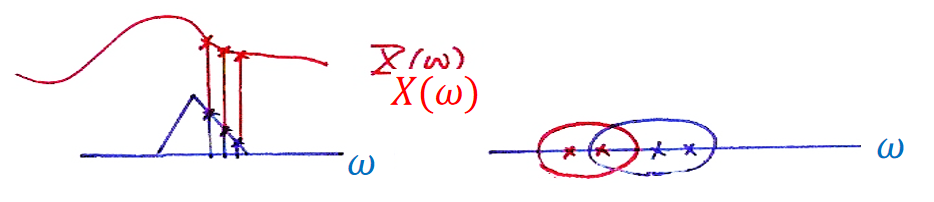
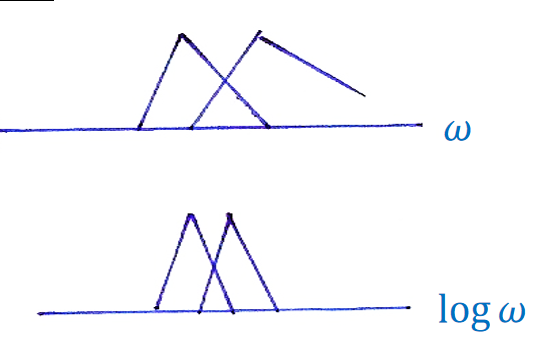
具体来说,MFCC流程图如下,先FFT再log(和求倒谱一样的思路),然后施加不同宽度的三角波,但是实际上我们是也可以通过改变横轴尺度来实现,这就叫Mel-Scaling。最后,不同于倒谱的是,我们求DCT而不是求IFFT来得到MFCC。
使用DCT的好处有:
- 比FFT更简单
- 得到的是实数值
- 能聚焦不同频段的能量
- 能减少维度
在进行DCT之后,我们取前12到13个数字作为特征(这些参数包含了大部分的信息),并且我们还求这些数字的一阶导数和二阶导数,总共加起来每个音频帧的MFCC有39个参数。
graph LR
A[原始音频信号] --> B[FFT]
B --> C[Log]
C --> D[Mel-Scaling]
D --> E[离散余弦变换 DCT]
E --> F((MFCC))

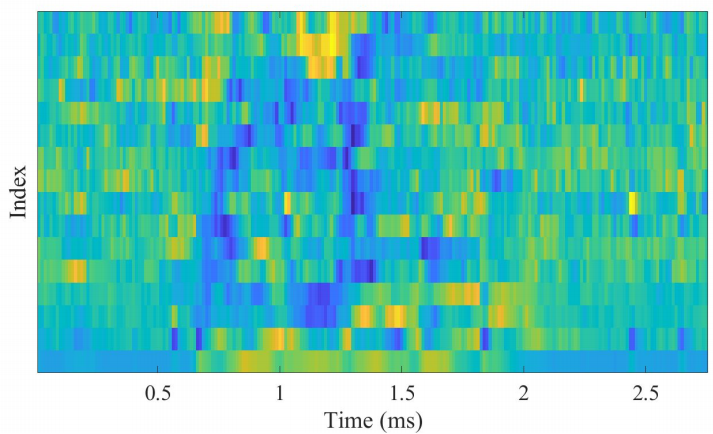
最后,我们可以可视化MFCC如下图
参考资料:
语音信号处理(第3版) 赵力等 机械工业出版社
台湾大学公开课 數位語音處理概論 李琳山 教授
MFCC特征提取教程 - 李理的博客 (fancyerii.github.io)
Mel-Frequency Cepstral Coefficients Explained Easily - YouTube