本文最后更新于：2023年1月8日上午

我的机器学习课笔记 #2-线性模型

[TOC]

线性模型就是一个通过属性的线性组合来进行预测的函数。下式中(1)(2)(3)都是线性的，而(4)不是线性的，因为看中的是学习参数 $w$ 的线性，而不是属性本身的变化是不是线性。

线性模型的优点是可解释性强，缺点是拟合能力比较弱，这一章使用线性模型进行回归和分类任务。

线性回归

线性回归的目标如下，最小化所有样本的预测结果与真实结果之间的欧几里得距离，即最小化均方误差（MSE）。

f(x_i)=wx_i+b，f(x)\approx y_i

argmin(\sum_{i=1}^{m}(f(x_i)-y_i)^2)

求解w、b有两种方法，一是通过最小二乘法可以得到w和b的最优解，二是通过梯度下降法迭代求导较优解。最小二乘法虽然能够一次求解，但是适用范围窄、当特征维度大时计算量比较大；梯度下降法是深度学习中最普遍的方法，面对成千上万的特征维度仍然能够很好求解。

最小二乘法

最小二乘法要求损失函数是凸函数，当损失函数的导数为0的时候认为达到了最优点，通过这个方程解出w和b的值。

对数线性回归

有时逼近的不是y而是y的衍生物，比如逼近y的对数： $\ln y=wx_i+b$

这种严格来说不是线性回归，而是广义线性模型的一种，广义线性模型需要一个单调可微函数 $g(·)$
$广义线性模型： y=g^{-1}(w^Tx+b)$

线性回归改进——正则化

为了抑制线性模型的过拟合，可以通过在损失函数中添加L1范数或者L2范数来进行正则化，对应LASSO回归和Ridge岭回归。

L1范数就是 $||w||_1=\sum^{d}_{i=1}|w_i|$ ，即向量w所有元素的绝对值的和

L2范数就是 $||w||_2=\sum^{d}_{i=1}w_i^2$ ，即向量w所有元素的平方的和

如图，使用时通过超参数 $\lambda$ 与原来的损失函数相加构成新的损失函数

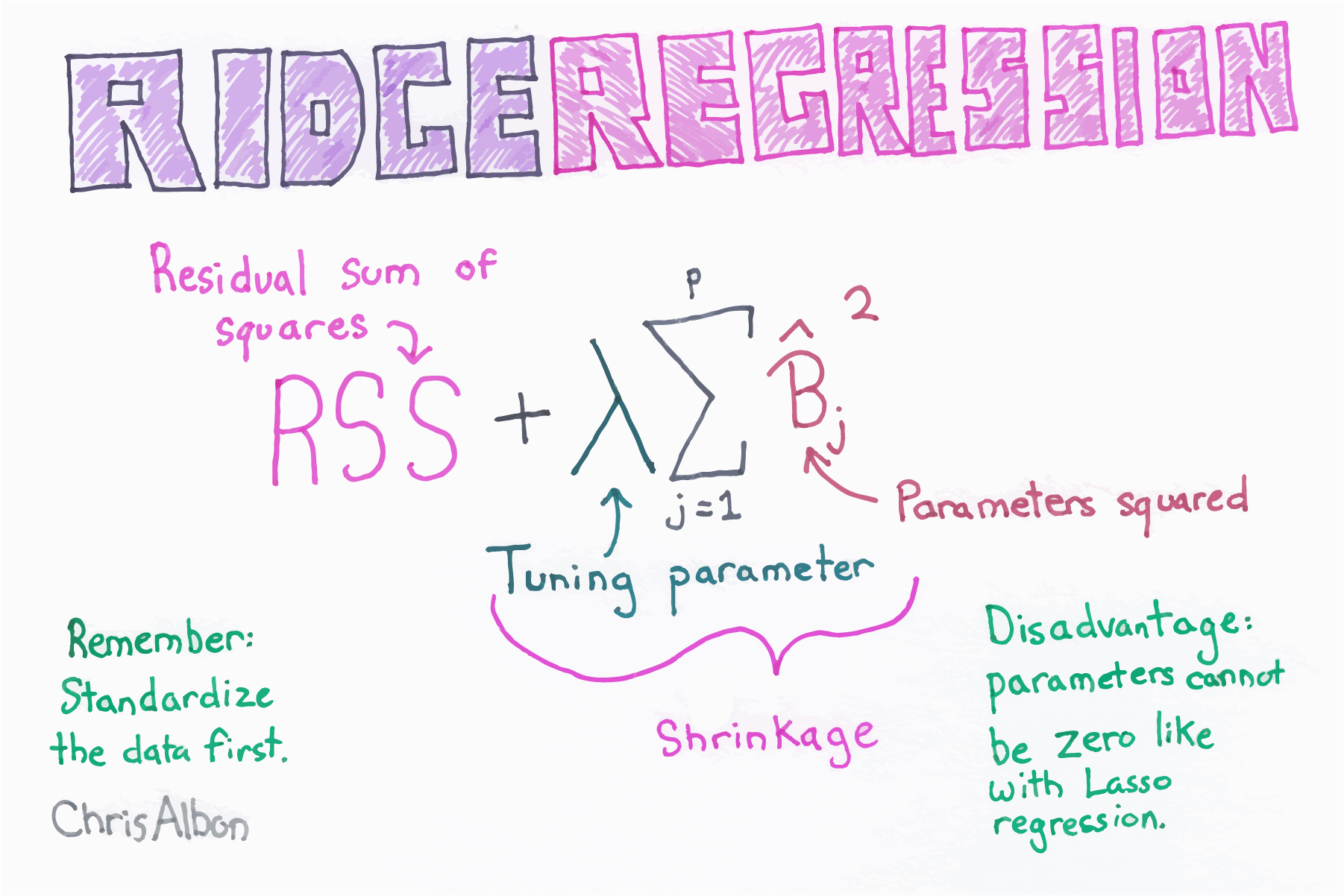
Ridge_Regression

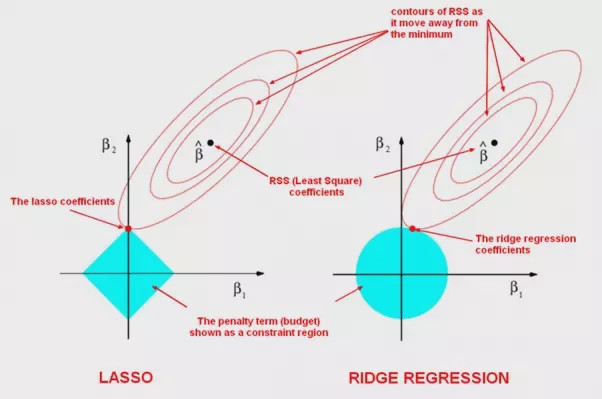
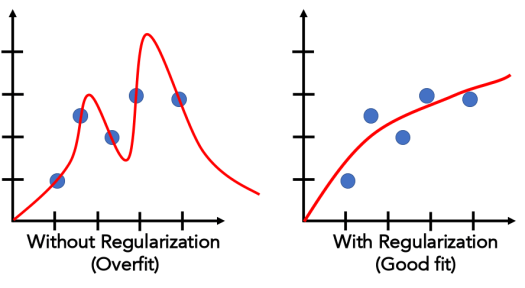
正则化抑制过拟合的原理是惩罚过大的w项，w太大会导致那么拟合曲线斜率就会更大、更不平滑，在损失函数中加上正则化项后w变大会导致损失函数变大，而我们的算法会让损失函数尽量小，从而得到更小的w，进而抑制了过拟合。两种正则化的对比如图，椭圆中心是原来loss的最低处，现在会往原点靠，得到的拟合效果如图，能较好的抑制曲线一上一下的过拟合情况。

线性分类（对数几率回归、逻辑回归）

假如做的是二分类任务，那么要输出的就不是一个值而是0/1了，即 $y\in \{0,1\}$ 。要把 $wx_i+b$ 的回归值转换成0/1，理想使用阶跃函数，但是因为不连续而不利于计算。所以需要找到一个决策函数 $g(·)$ 来近似，要求单调可微分，发现sigmoid函数（也叫对数几率函数 logistic function）符合条件。这个函数满足单调可微，而且形式简单，值位于0到1之间，预测时大于0.5的判为正例，小于0.5的判为负例。

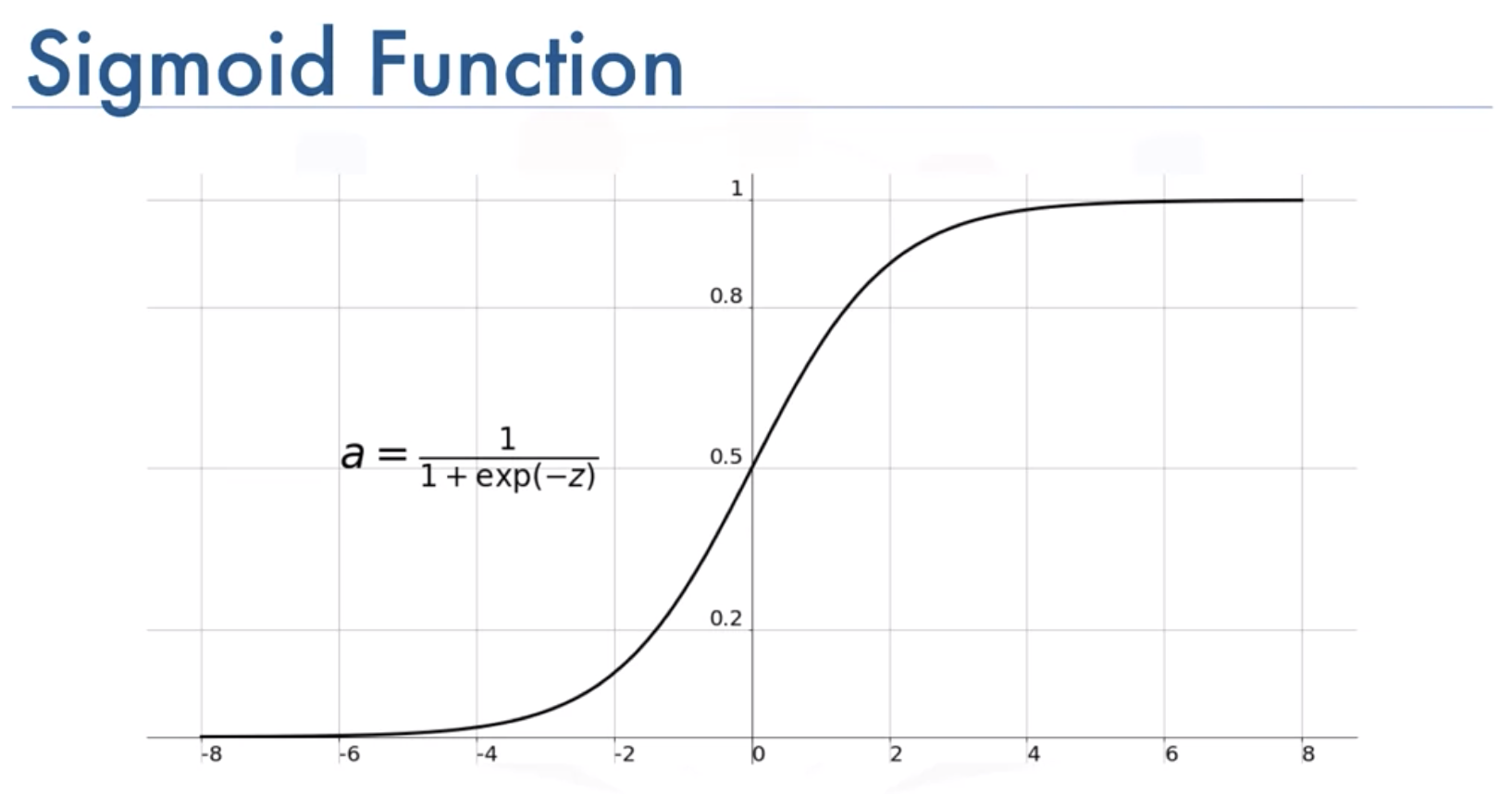
Sigmoid函数

为什么叫他对数几率回归呢，因为把函数形式变换一下就可以看做 $\ln{\frac{y}{1-y}}=w^Tx+b$ ，近似 $\frac{y}{1-y}$ 这个“几率”的对数。此处“几率”是 $\frac{发生概率}{不发生概率}$ 。

机器学习三要素的“模型”已经有了，接下来是损失函数，二分类问题的损失函数不使用MSE而使用对数似然函数。为什么不使用MSE呢？一是因为用MSE计算sigmoid出来的概率和标签时，MSE不是凸函数（这个想证明但是不会证）；二是会出现梯度消失，证明如下。

MSEloss的值用E表示，用标签 $y_i$ 减去 $\sigma$ 出来的概率，再求平方，然后对loss求偏导如公式所示，当 $\sigma$ 接近 $y_i$ 时， $\sigma$ 和 $1-\sigma$ 总有一个趋近于0，此时梯度消失。举个例子：当y=1时，预测出来σ=0.00001，此时距离真实值很远，应该梯度很大，然而梯度接近0。