我的机器学习课笔记 #1-绪论与模型评估

[TOC]

没有免费午餐定理（no free lunch theorem, or NFL）

人们使用机器学习是期望机器学习到的算法有用，但是NFL定理却证明，对于任意两个学习算法，它们的期望性能都一样。但是别灰心，NFL定理的前提是“所有情况下”，所以NFL说的是“一个算法不可能在任何情况下都取得最好的性能”。

但是我们并不需要一个算法在任何情况下性能都最好，甚至，我们经常只关注一个算法在一个方面的性能，比如使用鸢尾花数据集进行分类预测时，我们假设数据集中的4个属性足够让我们将鸢尾花进行分类，但是实际上鸢尾花有许多许多许多的属性，要将这些属性都综合考虑在内才能在所有情况下正确预测，所以用这个数据集训练出来的模型在其他鸢尾花数据集上可能就不工作了。

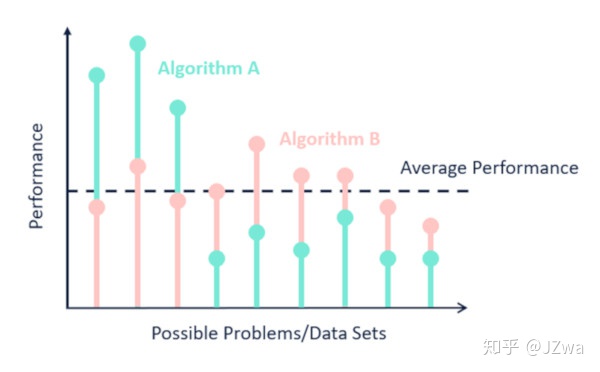
或者NFL定理也可以理解为“你不可能在没有假设的情况下从数据中学习”，如下图，我们的机器学习模型在学习过程中对于输入和输出作出了假设，这种假设可能在某些数据集上适用，但是换成别的数据集就不适用了。比如我有一个处理视频的模型，它假设视频中有物体运动的时序信息，但是视频中也可能没有运动，也可能是个意义不明的所有帧像ppt那样排布的视频，在这些情况下假设失效。

模型评估

对一个模型的评估会分成两类，一类是训练误差，另一类是泛化误差。前者是在训练样本上进行评估得到的误差，后者是在新样本上进行评估得到的误差。

这两类误差的大小能导致过拟合和欠拟合现象，如下表和下图，

	泛化误差大	泛化误差小
训练误差大	欠拟合	不可能
训练误差小	过拟合	模型的目标

如何得到训练误差和泛化误差呢？可以分为得到训练集和测试集的方法和使用哪种误差函数这两个问题。

如何得到训练集和测试集？

• 留出法

  最常用，就是把数据集的划分成两个互斥的集合，一个训练一个预测。

• 交叉验证法

  小样本适用，因为会带来更大的计算开销。K折交叉验证指的是将数据集随机分成K份，进行K次训练和预测，每次训练选取K-1份作为训练集，每次预测选取剩下那1份作为测试集。

• 自助法

  适用于集成学习，不会减少训练集的数据数量，但会改变数据集的分布。就是将一个拥有m个数据的数据集进行放回抽样，抽m次出来得到的就是训练集，用所有数据去掉训练集就是测试集，易知训练集的数量是m，但里面会有重复的数据。

使用哪种误差函数？

误差函数有很多很多种，作用就是告诉你模型的性能。西瓜书上主要介绍的是分类任务的性能度量。

错误率和精度

错误率就是分类错误样本占总数的比例，精度又叫做正确率、准确率（accuracy）。

混淆矩阵

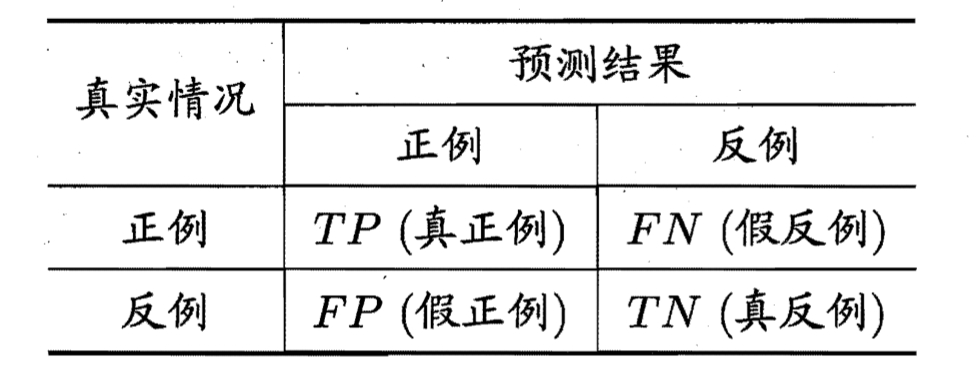
对于二分类结果，通常列出下面这种混淆矩阵，注意这个表的纵轴是真实情况，横轴是预测结果，有的图可能会把横纵轴对换，但是字母是不变的。

结果中的T/P指的是预测是否正确，而P/N指的是预测的是正例还是反例。FP就是预测是正例，但是预测错了，实际是反例，以此类推。

查准率、查全率、P-R曲线、F1

查准率查全率可以用搜索引擎的角度来解释，查准率就是搜索出来的数据有多少是对的，查全率就是有多少对的数据被查出来了，两者分母不同。也可以把查准率叫做精确率（和acc准确率区分开），把查全率叫做召回率。

$$查准率、精确率：Precise=\frac{TP}{TP+FP}$$

$$查全率、召回率：Recall=\frac{TP}{TP+FN}$$

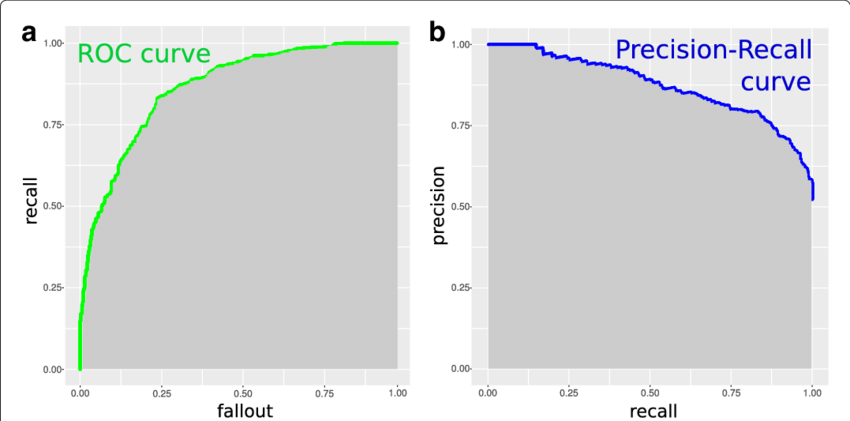
P-R曲线就是纵轴P，横轴R的曲线。分类问题一般会对测试数据得出一个预测概率，从高到低排序，可以手动选择最高的k个作为预测正例，在k不确定的时候，查准率和查全率就会呈现P-R曲线。假如k很大，那么查全率就会高，查准率就会低，因为把很多低概率的结果都判成正例。

查准率和查全率是对于模型两方面的评估，但是我们想要一个综合的评价指标，于是使用调和平均得到F1这个指标。

$$\frac{1}{F1} = \frac{1}{2} (\frac{1}{P}+\frac{1}{R})$$

若对于查准率和查全率需要偏好，则可以使用加权调和平均。

$$\frac{1}{F_\beta} = \frac{1}{1+\beta^2} (\frac{1}{P}+\frac{\beta^2}{R})$$

调和平均：参考如何理解与应用调和平均数？ - 知乎 (zhihu.com)

考虑一次去便利店并返回的行程：

• 去程速度为30 mph
• 返程时交通有一些拥堵，所以速度为10 mph
• 去程和返程走的是同一路线，也就是说距离一样（5英里）

整个行程的平均速度是多少？如果不假思索地应用算术平均数的话，结果是20 mph（(30+10)/2）。

但是这么算不对。因为去程速度更快，所以你更快地完成了去程的5英里，整个行程中以30 mph的速度行驶的时间更少，以10 mph的速度行驶的时间更多，所以整个行程期间你的平均速度不会是30 mph和10 mph的中点，而应该更接近10 mph。

用调和平均数呢？2 / (1/30 + 1/10) = 15 mph 一下子得到了真正的行程平均速度，自动根据在每个方向上使用的时间进行调整。

ROC和AUC

用查准率查全率得到的P-R曲线和F1指标有一个缺点，那就是都没用上混淆矩阵中的TN——也就是“真反例”——也就是预测是反例，真实是反例的结果。所以定义FPR为“假正例率”，ROC就是以FPR为横轴，召回率为纵轴的曲线。

$$FPR=\frac{FP}{TN+FP}$$

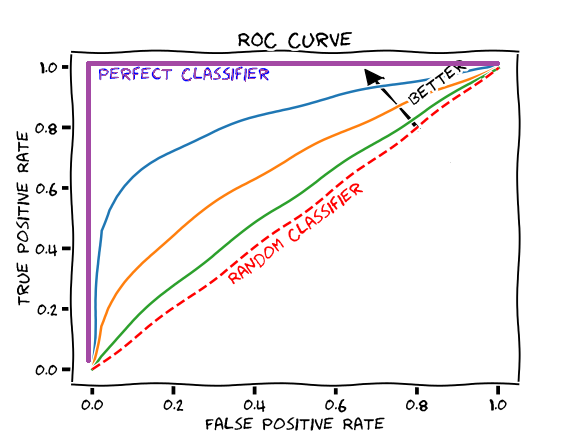
对于ROC曲线，越往左上角凸的模型越好，理解为“所有负例中被判错的少，且所有正例中被判对的多。”

然而P-R曲线和ROC曲线都有一个问题，那就是曲线之间不好准确比较，对于交叉的曲线无法判断孰优孰劣。所以将ROC曲线下的面积AUC作为单个数字的指标。

模型性能分析

得到模型的泛化误差后，我们仍然想知道如何模型为什么会得到这样的性能，于是我们对模型的泛化误差进行分析，可得：

$$泛化误差=偏差(bias)+方差(var)+噪声(noise)$$

• 偏差指的是模型算法本身的拟合能力，是预测结果与真实结果的偏离程度
• 方差指的是模型对于相同大小的训练集的学习结果的抖动。
• 噪声是和数据集本身有关的泛化误差的下界，即学习本身的难度。

假如是图片识别猫狗的二分类问题，在模型还没训练的时候，模型瞎猜能得到50%的正确率，无论训练集测试集怎么划分肯定都大概是这个结果，此时正确率低反映偏差高、数据划分不带来结果变化反映方差低；在模型训练很久之后，模型会对训练集拟合得越来越好，此时正确率上升，偏差也随之下降，但是也可能学习到训练集中的特殊信息，导致过拟合，此时方差高。

参考文献：

周志华的西瓜书

Machine Learning’s No Free Lunch Theorem Explained (analyticsindiamag.com)

No free lunch theorem-没有免费的午餐 - 知乎 (zhihu.com)