The Platonic Representation Hypothesis

论文链接：The Platonic Representation Hypothesis (arxiv.org)

项目主页：The Platonic Representation Hypothesis (phillipi.github.io)

代码链接：minyoungg/platonic-rep (github.com)

MIT团队发表的一篇ICML 2024论文，被ChatGPT之父Ilya Sutskever点赞过，对于大模型的未来提出了柏拉图表征假说（Platonic Representation Hypothesis），本文简单介绍这篇论文的观点和证明思路。

什么是柏拉图表征假说

目前，随着LLM的发展，各个领域的模型正在逐渐统一，多模态统一的模型越来越多，这些模型的架构和能力正在越来越相似。这篇论文根据这个趋势提出了Platonic Representation Hypothesis（PRH）：

Neural networks, trained with different objectives on different data and modalities, are converging to a shared statistical model of reality in their representation spaces.

翻译：无论神经网络使用什么样的目标函数、数据集、模态（任务），它们都将在表征空间中收敛到一个共享的现实的统计模型。

如上图所示，假定存在一个现实世界$Z$，它可以通过拍照、触摸等方式映射到图像$X$或者文本$Y$空间，不同的表征学习模型在$X,Y$这种模态上学习表征，而作者认为这些模型在训练的时候，不得不学习越来越多关于$Z$的知识，从而不同的模型都在往$Z$收敛。并且，这种收敛会随着模型大小、任务多样性、数据量的增大而加快。

也许你也发现了，这个假说有着重要的限制。它假设了$Z \rightarrow X$的这种映射是一种双射，比如每一个现实中的事件能够与一个图像对应，反之亦然。但是这个假设不一定成立。文章后续有对此的讨论。

PRH与柏拉图和其它理论的关系

柏拉图洞穴假说

柏拉图在《理想国》的第七册中提出了洞穴假说（The allegory of the cave）。想象有一些人生活在洞穴之中，他们从小在洞穴，手脚脖子都被束缚住，导致他们只能看见面前的岩壁。再想象他们后面又一个火堆，能够将光打在岩壁上。当有人从后面经过时，他们能看见岩壁上的影子，当有人在后面说话时，他们会认为岩壁上的影子在说话。他们无法想象他们在一个洞穴之中，在洞穴外有河流、有太阳、有一切，他们只会认为他们面前的影子就是他们的世界。

表征学习模型的训练数据就是岩壁上的影子。

作者假设对这些影子的学习能够毕竟洞穴外的真实世界。

科学实在论

这是一种哲学，科学实在论者认为科学理论是实在的，原子、电子、量子、电磁场是实在的，各种理论描述的状态和过程都是真实存在的。

这么说可能有一些抽象，举一个反对者的观点吧：以太理论、日心说在曾经盛行，被认为是正确的，但是现在都认为那些理论是错的，那我们又如何得知我们目前的理论体系是对的呢？我们又怎能确保原子电子存在呢？

具体怎么争辩的，我也不懂，但是科学实在论大概是认为科学正在逐渐接近真理，即便我们很多时候只能进行片面的实验。

这种论调就也类似PRH，我们对人类所感知世界的研究会接近世界本身的真理，神经网络对映射后数据的学习也能够接近世界本身的统计规律。

安娜·卡列尼娜

托尔斯泰在《安娜·卡列尼娜》的开头写道：幸福的家庭千篇一律，不行的家庭各有各的不幸。

这句话被人归纳为Anna Karenian Principle（AKP），安娜·卡列尼娜原理。即幸福的家庭有共同的特质（健康、恩爱、富裕），这些特质带来幸福，但是只要有一项不满足，那就会导致不幸。

PRH认为”幸福的表征“就是满足了各种特质后收敛的那个神经网络。幸福特质表示数据集，假如神经网络对数据都有比较好的解，那就认为满足了幸福特质，而这些神经网络都会”千篇一律“。比如MAE预训练的模型和CLIP预训练的模型在图像数据集上都能得到很好的效果，然后PRH认为他们得到的特征会比较相似。

PRH的调研方法

• representation 表征，是一个函数：$f: \mathcal{X} \rightarrow \mathbb{R}^n$，对于某个数据域$\mathcal{X}$​中的每一项都分配一个特征向量。
• kernel 核 用来表示不同数据点的距离/相似度是如何计算的：$K: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}$，其中$K(x_i,x_j)=<f(x_i),f(x_j)>$，$<\cdot,\cdot>$是点积操作，且$K \in \mathcal{K}$。
• kernel-alignment metric 核对齐指标 用来衡量不同kernel的相似度：$m: \mathcal{K} \times \mathcal{K} \rightarrow \mathbb{R}$。

PRH使用了一个叫做mutual nearest-neighbor metric的核对齐指标，在附录A有这个算法，比较简单：

在数据集/数据分布$\mathcal{X}$中，对于每一项分别用两个模型$f,g$提取特征，假如是同一个模态，则$f,g$都是相同模态的模型，且他们输入的数据是一样的，假如是两个模态，那$f,g$就是不同模态的模型，他们输入的数据就是数据对，比如图像-文本对。对于每一个数据对的特征，我们计算他们的$k$个最近邻，然后最近邻的交集除以$k$就是指标。假如$f \approx g$，那么距离某个样本$x_i,y_i$接近的样本应该也都类似，比如$x_1,x_6,x_8|y_1,y_7,y_8$的交集就是1号和8号，那指标就是$2/3$。

PRH通过这种方式来衡量不同模型之间的相似度。

下面介绍这篇文章的发现：

表征正在收敛！！！

这是论文的第二章，给出了以下5个发现：

1. 不同的模型，无论架构、目标，可以拥有对齐的表征
2. 表征的对齐程度随着模型规模和性能而上升
3. 表征正在跨越模态收敛
4. 模型与大脑正在对齐
5. 越对齐，下游任务越厉害

对于结论1，作者进行了文献调研。一种Model stitching的方法将$f$的前几层和$g$的后几层拼接在一起，假如拼接后的模型效果号，那么说明$f,g$比较兼容。Model stitching的论文发现ImageNet上预训练的模型和Places-365上训练的模型比较兼容；还发现early的卷积层比其他层更兼容。另一篇论文发现英语语言模型和法语语言模型在对方任务上做zero-shot性能也不错。还有一篇论文发现了罗塞塔神经元（Rosetta Neurons），这种神经元形成了一个词表，在所有模型中都发现了这个词表。

对于结论2，观察下图，左图横轴是一个评价指标，越高表示模型在视觉上性能越好，纵轴是一个bin内的模型的互相的对齐程度。右图则是UMAP的可视化，展示了不同模型之间的对齐情况，越蓝色性能越好，越近越相似。他们发现性能越高的模型，他们特征也越相似。

对于结论3，观察下图，他们衡量了5个视觉模型和一批语言模型的对齐，参数量越大的模型，语言性能越好，同时与视觉模型的对齐程度也越高，并且呈现了线性的关系。其中多模态预训练的CLIP对齐结果更强，但是IN21K微调之后就不那么强了。

对于结论4，作者主要调查了其它学科的一些文献。

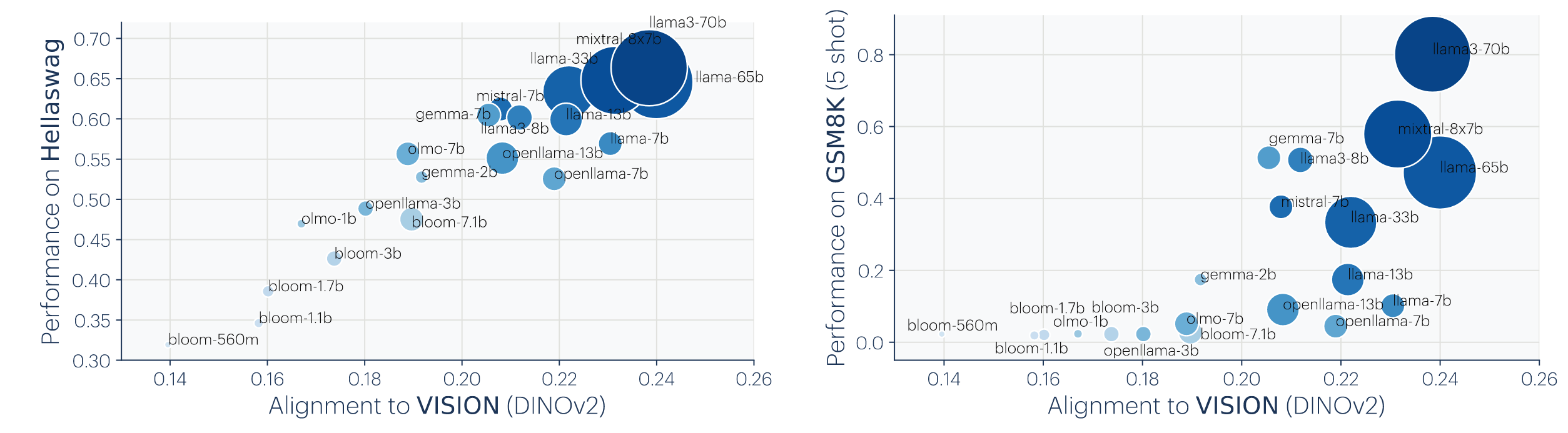
对于结论5，观察下图Hellaswag是常识评价数据集，GSM8k是数学数据集，分别都展示了类似的结论，即与视觉越对齐，在下游任务性能越高。但是Hellaswa呈现线性，GSM8k呈现”涌现“。

为什么表征收敛？？？

上面这个公式大家都比较熟悉，训练好的最优模型$f^*$是在参数空间$\mathcal{F}$中的结构风险最低的那个函数。结构分享包含了一个期望和一个正则项，期望就是对于数据集分布中的所有数据，你设计的loss最小，正则项就是dropout这样的限制。

论文从上面着三种颜色来说明为什么表征会收敛。

训练目标

论文提出了多任务假设，即：模型训练的任务越多，那么解的范围也就越小。观察下图比较直观，两个椭圆表示两个任务下较低的区域，要同时解决两个问题，那么面积就是他们的 交集，就一定是更小的。

模型容量

就是参数量，作者认为更大的模型更有可能收敛到相同的表征。如下图所示，更大的模型才会有更多的解，才更可能有交集。

Simplicity bias

更大的模型更倾向于找到对于数据来说最简单的拟合。我们会增加正则项，让模型朝着简单的方向收敛。

综上所述，模型越大，就越有可能找到共同的解，训练目标越多，解的范围就越小，在共同的解范围内，又会朝着简单的方向收敛，所以表征收敛。

我们将收敛到什么样的表征？？？

PRH说神经网络将收敛到一个现实的统计模型，但是这个统计模型到底是什么呢？

假设世界由一系列离散的事件组成$\boldsymbol{Z} \triangleq [z_1,\dots,z_T]$，并是从一个未知的分布$\mathbb{P}(\boldsymbol{Z})$中采样而来的。每一个事件可以通过不同的方式观测到，论文假定这种观测是双射(bijective)且确定的的函数：$\text{obs}:\mathcal{Z} \rightarrow \cdot$，将事件映射为一个任意的空间，比如像素、声音、质量、力、单词、力矩等等。本身事件可以直观地被认为是世界在“某时”的一种状态（也可以是空间），但是我们还是不要那么深究，就把它当作没有物理意义的一个东西吧。假如我们知道了$\mathbb{P}(\boldsymbol{Z})$，那我们就能够预测很多东西，我们就可以构建一个世界模型。

作者认为对比学习模型能够收敛到$\mathbb{P}(\boldsymbol{Z})$，并解释如下：

$$P_{\text {coor }}\left(x_a, x_b\right) \propto \sum_{\left(t, t^{\prime}\right):\left|t-t^{\prime}\right| \leq T_{\text {window }}} \mathbb{P}\left(X_t=x_a, X_{t^{\prime}}=x_b\right) .$$

在世界的某个时间窗口内发生了一个事件的两个观测$x_a,x_b$，上面是他们的共现概率。现将positive pair定义为两个发生时间很近的观测，negative pair则为任意采样的观测。对比学习模型需要学习一个表征：$f_X:X\rightarrow \mathbb{R}^d$，从而：

$$\left\langle f_X\left(x_a\right), f_X\left(x_b\right)\right\rangle=K_{\mathrm{PMI}}\left(x_a, x_b\right)+c_X,$$

其中PMI是pointwise mutual information，点对点互信息，就是$\log\frac{P(x,y)}{P(x)P(y)}$。所以，对比学习的模型是通过$K_{PMI}$这个核来最小化的。

既然我们考虑了观测$x_a,x_b$符合上式，并且观测是双射函数，所以$K_{\mathrm{PMI}}\left(x_a, x_b\right) = K_{\mathrm{PMI}}\left(z_a, z_b\right)$，进一步有：

$$\begin{aligned} K_{\mathrm{PMI}}\left(z_a, z_b\right) & =\left\langle f_X\left(x_a\right), f_X\left(x_b\right)\right\rangle-c_X \\ & =\left\langle f_Y\left(y_a\right), f_Y\left(y_b\right)\right\rangle-c_Y \end{aligned}$$

所以对于任意模态，都会发现表征将收敛到同一个kernel，也就是说表征学习旨在找到相似度=PMI的特征空间。

颜色研究

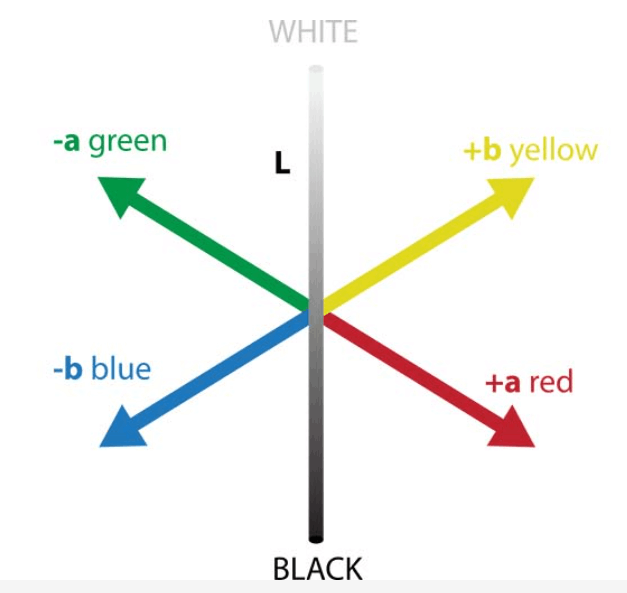
为了证明收敛在真实数据上可行，作者从用语言模型来推理颜色之间的距离，并进行了可视化：

其中最左边是CIFAR-10数据集中的颜色在CIELAB颜色空间中的可视化，VISION那一栏是CIFAR-10数据集上统计了每种颜色对于其它颜色共现概率的可视化，假如一个颜色出现在另一个颜色的4个像素内，就算共现。LANGUAGE那两栏就分别是对比学习模型和生成式模型的例子，可视化了颜色的单词在语言空间中互相之间的距离，可以发现仅在语言模态学习的对色彩的理解，和人真实对色彩的感知是接近的。

直观来说，就是一个人只看书上对颜色的描写，就能知道颜色大概都是什么样的。

PRH能给我们带来什么样的结论？

这里就不解释了，大家可以参考原文

1. 扩大训练规模来拟合可行，但是也有其它更高效率的方法
2. 训练数据可以在不同模态间共享（假如你想有一个牛逼的视觉模型，那你不能只用视觉数据训练，还应该用其它模态的训，比如CLIP比ImageNet预训练的强）
3. 不同模态模型之间的迁移和适配将更简单（模型越来越收敛，那么表征就越相似了）
4. 扩大规模可能能够降低大模型幻觉和偏见（对于偏见，比如说语料库中对黑人的歧视这些，作者认为不会消除，而是说模型会更加准确地体现现实世界或者训练数据的bias）

PRH的限制

1. 不同模态可能包含不同的信息，文本中“I believe in the freedom of speech”这句话就很难用图像来表达。这一点和作者的“bijective”假设息息相关，因为这种双射假设很可能不成立。
2. 这篇论文主要研究视觉和语言，其他模态研究比较少。
3. AI模型的发展受到AI从业人员的偏见以及硬件发展的引导，从而在收敛路上造成bias
4. 对于特定小领域的AI，可能没有收敛。
5. 测量方式使用的mutual nearest-neighbor有待商榷
6. 上面一些图表示不同模态的模型的匹配度虽然有增长，但是还是很低，要是是噪声怎么办？

结尾

最后还是很推荐大家去看一下这篇文章，对深度学习未来的发展有新的理解。