学习笔记 Gumbel-Softmax分布

Gumbel-Softmax Trick是一种常用于将离散随机变量（例如分类任务中的类别）转化为连续随机变量的技巧，又被叫做Concrete分布。这个技巧最早被应用于生成模型中，特别是针对离散输出的生成模型。本文是学习这种技巧的学习笔记。

参考文献：

这篇知乎写的很好：Gumbel softmax trick （快速理解附代码） - 知乎 (zhihu.com)

大佬博客：What is Gumbel Softmax? - Luyuan’s Blog (wangluyuan.cc)

The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables (vitalab.github.io)

同时也问了问chatGPT

什么是Gumbel分布

Gumbel分布是一种极值分布，常用来建模极端事件的分布（最大风速、最大降雨量等）

$$f(x;\mu,\beta) = exp(-exp(\frac{x-\mu}{\beta}))$$

参考文献里知乎文章举的例子是这样：高中有16个人数很多的班，每个班抽30人，这30个人的身高应该服从正态分布。现在从每个班的30人中选出身高最高的人，这16个人就服从Gumbel分布。

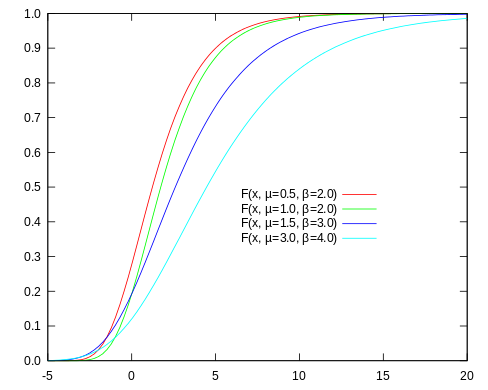
ChatGPT的例子：现在收集了某个城市多年来的每天降雨量数据，为了估计极端降雨时间的概率，可以用Gumbel分布来估计。先统计出20年来每年的最大降雨量数据，然后根据这些数据通过极大似然估计等方法，估计Gumbel的$\mu,\beta$参数。有了参数之后，就可以根据上面这个累积分布函数（CDF）来求出降雨量大于某个值的概率：$P(320 \le x) = exp(-exp(-\frac{320-\mu}{\beta}))$

当$\mu=0,\beta=1$时为标准Gumbel分布：$F(x)=e^{-e^{-x}}$

什么是Gumbel Softmax

知乎文章的例子：考虑一个K分类任务，假设用MLP学习到了一个K维的向量$\boldsymbol{h}$，若直接做推理的话，那就直接取$y=\arg max \boldsymbol\ {h}$。但是我们一般还要赋予概率上的意义，比如使用softmax函数作用于$\boldsymbol h$来获得概率$\boldsymbol p = softmax(\boldsymbol h),\ p_i \in [0,1]$。获得概率分布之后，直接得到离散变量就是直接去argmax（取最大值的过程像Gumbel）。

然而我们期望根据概率进行采样，所以接下来我们添加Gumbel噪声：$\boldsymbol{p^g}=log(\boldsymbol{p} + gumbel\_noise)$，添加了噪声之后，概率就会发生改变，取最大值（$\arg max\ \boldsymbol{p^g}$）作为类别的时候就可能根据概率发生变化，所以就会根据概率进行采样了。

但是在深度学习中，还要满足求导的要求，argmax是无法求导的，所以改成softmax：$softmax(\boldsymbol{p^g}/\tau)$，其中$\tau$是温度。在更新参数的时候，softmax可以求导，$\boldsymbol{p^g}$也可以求导，其中的gumbel noise就当作常数就够了。

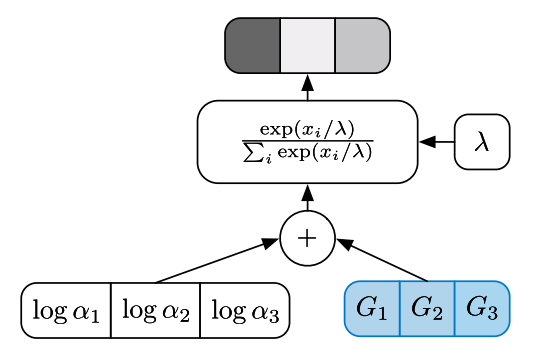
大佬博客：为什么选择选择 Gumbel Noise 呢？数学上可以证明对每个值加上一个独立标准 Gumbel 噪声后，取最大值，得到的概率密度和 softmax 一致。通过实验，也可以验证如果使用其他的噪声，概率会失真。具体的实验结果和数学证明可以参考这篇文章，证明过程还比较复杂。

Pytorch中的gumbel_softmax

torch.nn.functional.gumbel_softmax — PyTorch 1.13 documentation

这个函数就是把logits输入进去，然后输出一个概率，最大概率的那一项可能并不是ligits最高的那个，而是根据logits经过softmax之后的概率随机产生的。