论文笔记 两篇分析多头注意力的论文

本文介绍两篇分析Transformer中多头注意力的论文，第一篇促使不同head关注不同的地方，第二篇对每个head的重要性、功能进行分析，并依次对一些头进行剪枝。

论文1：Multi-Head Attention with Disagreement Regularization

论文2：Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned

1️⃣ Multi-Head Attention with Disagreement Regularization

多头注意力使Transformer能够关注不同位置的子空间表征，该文章提出了一种**“分歧正则化”（Disagreement Regularization）**的方式来显式地鼓励不同头关注不同的地方。

在Transformer中，输入$Q,K,V$假设为$d$维，每一个头的矩阵$W_h \in \mathbb{R}^{d\times d_k}$将输入映射到一个更低维度的子空间，得到$Q^h=QW_h^Q$（以Q为例，其余同理）。

为了让每个头关注不一样的信息，即增强多头的多样性，本文提出了三种正则化：

1. 子空间分歧正则化（Sub.）

   该正则化作用于值向量$V$上。输入的$V$会通过$V^h=VW_h^V$得到该头的$V^h$，然后所有头之间互相计算余弦相似度，然后用相似度的负数作为Loss。

   $$D_{sub}=-\frac{1}{H^2}\sum^H_{i=1}\sum^H_{j=1}\frac{V^i\cdot V^j}{||V^i||\ ||V^j||}$$

2. 关注位置分歧正则化（Pos.）

   该正则化用于QK相乘的注意力矩阵上。$A^h=softmax(\frac{Q^h {K^h}^T}{\sqrt{d_k}})$，然后所有头之间的注意力矩阵互相点乘来计算相似度，用负数作为Loss。

   $$D_{pos}=-\frac{1}{H^2}\sum^H_{i=1}\sum^H_{j=1}|A^i \odot A^j|$$

3. 输出分歧正则化（Out.）

   该正则化作用于注意力矩阵与V相乘之后的输出上。$O^h=A^hV^h$，然后和Sub.的计算方法一样：

   $$D_{sub}=-\frac{1}{H^2}\sum^H_{i=1}\sum^H_{j=1}\frac{O^i\cdot O^j}{||O^i||\ ||O^j||}$$

该文章用机器翻译作为实验的任务，将正则用在编码器的结果如下：

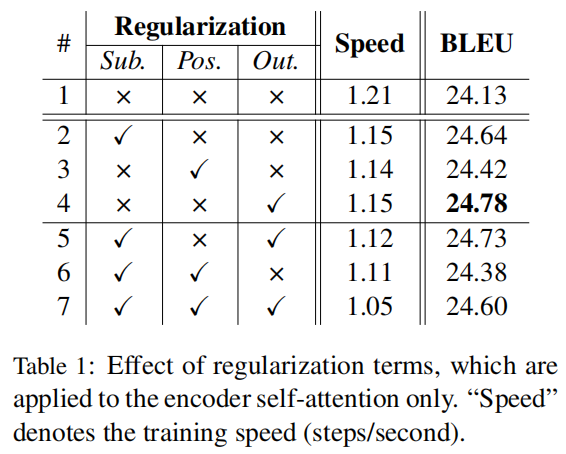
可以发现加上正则项之后，三个正则方法都提升了模型性能，但使速度有些下降。分析第2、3、4行，可以发现对输出进行分歧正则化的效果最好，对注意力进行分歧正则化效果最差。分析5、6、7行，发现同时使用多个正则项并不会带来更好的结果。

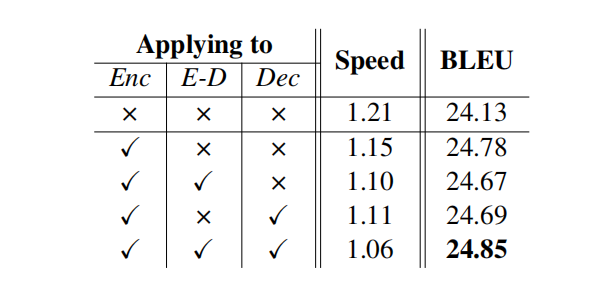
作者接下来又尝试了在不同模块加这个正则化，Enc表示在编码器的自注意力上加，E-D表示在交叉注意力上加，Dec表示在解码器的自注意力上加。然后发现都加最好，但是其中两个加上就不好……

（感觉作者实验少了，也不知道有没有多次实验取平均）

2️⃣ Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned

这篇文章发表在ACL2019上，研究了多头注意力的一些机制，如标题所述，论文的最终结论为是：多头注意力中，一些专业化的Head最重要，其余的可以被剪枝。

推荐阅读材料：

• YouTube演讲视频
• GitHub官方代码
• 官方blog

论文的故事分成三个阶段：

graph LR

A[Head's Importance] --> B[Head's Functions]
B --> C[Purning Heads]

Head’s Importance

这篇文章首先通过两种方式定义了head的重要性，第一种方式是head的confidence，它取模型自注意力的相似性矩阵的最大值，假如head越自信，那他就会越关注某个token。在一个集合的输入下进行平均，最后就能分析出每个头的自信度。

另一种方式是计算head的LRP，LRP是layer-wise relevance propagation，是引用另一篇文章的结果，这篇文章将其来评估哪一个头对于top-1 logit的贡献更高。具体算法见论文的附录A。

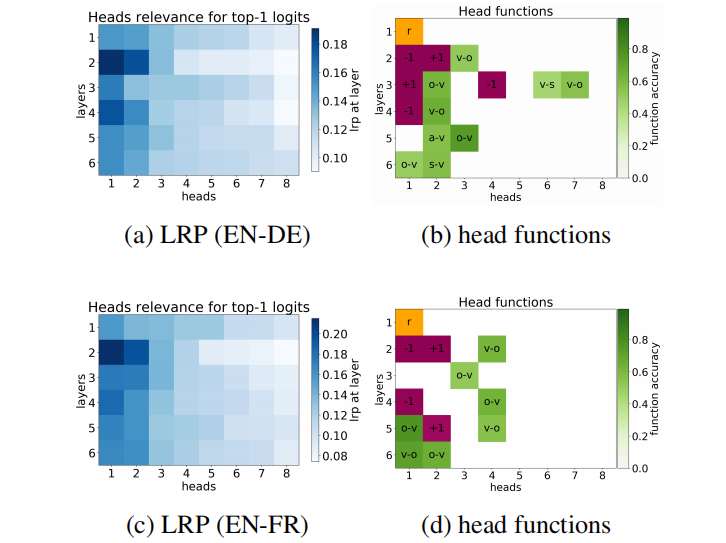
得出的结果如下图所示，可以发现两种方法得出的图相似，8个头中，有的头非常重要，而像第8个头最不重要，在6个层中的LRP和confidence都很低。

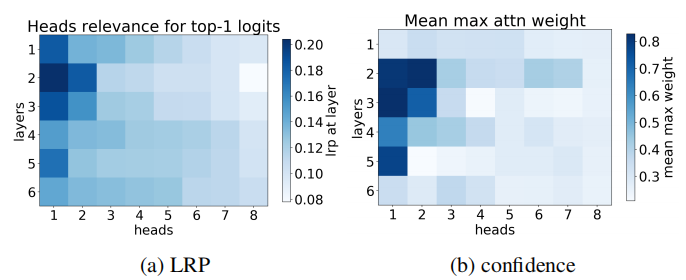
Head’s Functions

这一步用来分析每个head的功能，作者根据经验，将head通过注意力的分配方式分成三种：1. positional（相邻） 2. syntactic（句法） 3. rare words（稀有词理解）

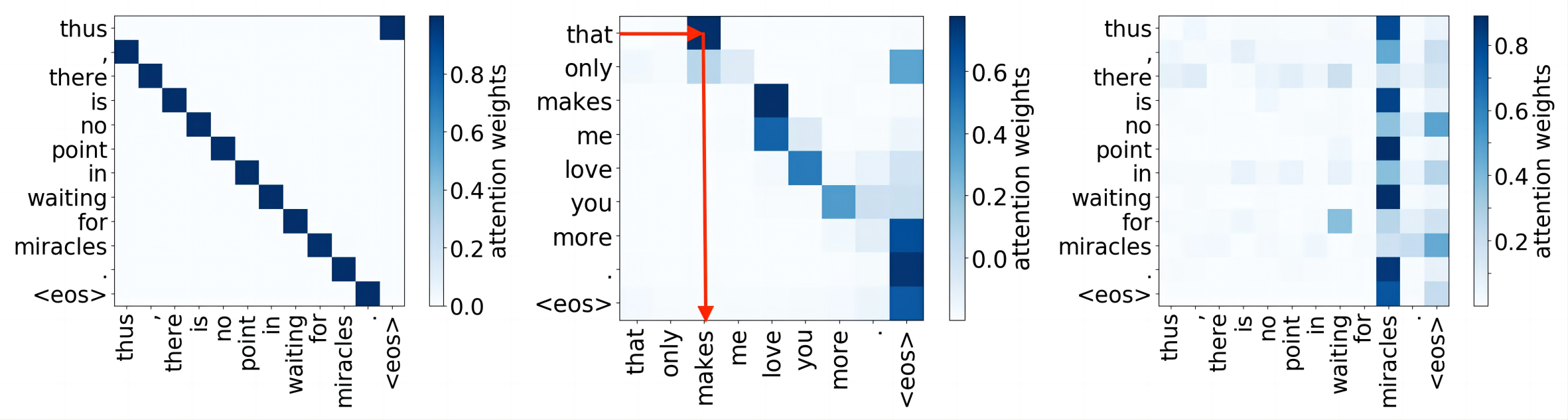
第一种表示该head得到的注意力矩阵主要让该token关注相邻的token，是上图最左边的图示。当至少90%的最大注意力被分配在相邻位置时，这个头就被定义为Positional Head。如下图2(b)(d)，里面+1和-1的地方就是，作者发现LRP最高的头往往就是Positional Head。

第二种表示注意力分配在句法上，比如上图中间的图示，一般认为Transformer的编码器负责理解句子单词之间的结构。作者进一步分成了多个关系：nominal subject，direct object，adjectival modifier，adverbial modifier。（不太懂语言学，但是大概就是词和词之间的关系，比如形容另一个词，修饰另一个词等。）如下图2(b)(d)中绿色的块。

第三种表示注意力分配在稀有词汇上，就是一个生词几乎吸引了所有注意力。作者发现在所有模型中第一层总有一个头是这种，比如下图2(b)(d)中的r块。

Pruning Heads

如上图2(b)(d)，仍然有很多白色的块，不属于任何类型，所以他们能够被剪枝吗？作者在多头注意力中添加了门控：

$$MultiHead(Q,K,V)=Concat_i(\textcolor{blue}{g_i} \cdot head_i)W^O$$

其中$g_i$是不依赖于输入，仅与head有关的参数，为了稀疏化，对$g_i$添加了$L_0$正则化（就是非0的个数）。然而$L_0$不可微分……所以论文这里使用Hard Concrete distributions方法来添加正则化。根据论文中的描述，就是将Gumbel-Softmax分布从原来的[0,1]范围扩展$\epsilon$，然后再clip到[0,1]，小于0的概率汇集到0上，大于1的概率汇集到1上。然后，非0参数的个数就能被用作L0正则化项了。

Hard Concrete distributions：参考资料、代码