图神经网络学习笔记：从GCN到GAT再到Relation-aware GNN

我学习图神经网络的入门学习笔记，本篇主要从图神经网络框架开始，介绍基础的图卷积神经网络（GCN），再介绍学习边注意力的图注意力网络（GAT），最后到与边种类有关的Relation-aware的图神经网络。

图神经网络的一般框架

图神经网络常用的基本框架是消息传递神经网络（MPNN），其基本思想是将图神经网络表示为节点间神经消息传递，有两个重要函数——消息函数（message）和更新函数（update）：

$$m_i^k=\sum_{i \in N(j)} \boldsymbol{M}_k(\boldsymbol{H}^{k-1}_i, \boldsymbol{H}^{k-1}_j, e_{ij}) \\ \boldsymbol{H}^k_i=\boldsymbol{U}_k(\boldsymbol{H}_i^{k-1},m_i^k)$$

$\boldsymbol{M}_k(\cdot,\cdot,\cdot)$表示消息函数，定义了第 $k$ 层中节点 $i$ 和节点 $j$ 的消息，其取决于第 $k-1$ 层的节点特征（$\boldsymbol{H}^{k-1}_i, \boldsymbol{H}^{k-1}_j$）以及这两个节点间的关系强度 $e_{ij}$。（$N(j)$表示节点 $j$ 的邻居节点）

$\boldsymbol{U}_k(\cdot,\cdot)$是第 $k$ 层的节点更新函数，其结合节点本身的特征和邻居节点的特征进行消息聚合。

图卷积网络（GCN）

论文链接：Semi-Supervised Classification with Graph Convolutional Networks (arxiv.org)

GCN核心公式如下：

$$\boldsymbol{H}^k_i=\sigma(\sum_{j\in N(i)} \frac{\boldsymbol{A}_{ij}}{\sqrt{\boldsymbol{\tilde{D}}_{ii}\boldsymbol{\tilde{D}}_{jj}}}\boldsymbol{H}^{k-1}_j \boldsymbol{W}^k + \frac{1}{\boldsymbol{\tilde{D}}_{i}}\boldsymbol{H}^{k-1}_i \boldsymbol{W}^k )$$

括号中，前一项计算节点 $i$ 的邻居传递的消息（即消息函数），后一项计算自己的消息。

前一项式中$\boldsymbol{A}$是图的邻接矩阵，与特征矩阵$\boldsymbol{H}^{k-1}$叉乘之后就会得到邻居节点的特征矩阵，分母表示对特征进行标准化，参考这篇博客，$\boldsymbol{\tilde{D}}_{ii}=\sum_{j}\boldsymbol{\tilde{A}}_{ij}$即邻接矩阵在行上的度，表示一个节点需要将接收到的其他节点的消息取平均（假如连接了5个节点则乘1/5），另一个则是在列上的度，直观来说。GCN希望有更多邻居的节点的影响更低，有更少邻居节点的影响更高。

自己和邻居的信息都经过一个可学习的参数矩阵$\boldsymbol{W}^{k}$进行变换，之后在跟一个激活函数来增强拟合能力，从而得到这一层的输出$\boldsymbol{H}^{k_i}$。

要注意的几点如下，①GCN每一层表示消息在图上传播一跳；②GCN对于不同邻居的权重仅来源于其连接的邻居数量；③GCN没有边的种类之分。

图注意力网络（GAT）

论文链接： Graph Attention Networks (arxiv.org)

在图中，两个节点间的强度可能并不能通过其连接数量反映出来，所以GAT对这一点进行改进，利用注意力机制，自动学习每个邻居节点的重要性。

对于两个节点，GAT先测量其注意力系数：

$$e_{ij}=a(\boldsymbol{W}\boldsymbol{H}^{k-1}_{i}, \boldsymbol{W}\boldsymbol{H}^{k-1}_{j})$$

其中$\boldsymbol{W}$是一个共享的变换矩阵，节点特征先经过变换，然后再经过注意力函数$a$来计算注意力系数。原文中这个注意力函数被定义为一个单层前馈神经网络，即拼接输入后一个全连得到值，得到的$e_{ij}$再归一化之后成为最终的注意力$\alpha_{ij}$，如原文中图所示：

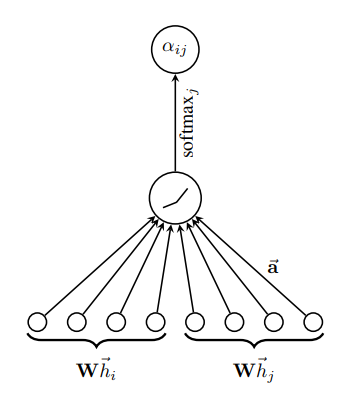
既然有了注意力机制，那也可以像Transformer一样引入多头注意力，即通过不同的变换矩阵计算出不同头的节点特征，然后求多头的平均（或者也可以用其他方式池化）。

同样，要注意的几点如下：①GAT每一层表示消息在图上传播一跳；②GCN没有边的种类之分。接下来要介绍的就是Relation-aware的图神经网络，这些网络能够处理图结构中不同边对节点的影响。

Relational Graph Convolutional Network（R-GCN）

论文链接：Modeling Relational Data with Graph Convolutional Networks (arxiv.org)

R-GCN就是在GCN的基础上进行改进，添加了对边种类进行建模的模型。将GCN和R-GCN的核心公式对比如下：

$$GCN: \boldsymbol{H}^k_i=\sigma(\sum_{j\in N(i)} \frac{\boldsymbol{A}_{ij}}{\sqrt{\boldsymbol{\tilde{D}}_{ii}\boldsymbol{\tilde{D}}_{jj}}}\boldsymbol{H}^{k-1}_j \boldsymbol{W}^k + \frac{1}{\boldsymbol{\tilde{D}}_{i}}\boldsymbol{H}^{k-1}_i \boldsymbol{W}^k )$$

$$RGCN:\boldsymbol{H}^k_i=\sigma(\sum_{r\in R} \sum_{j\in N(i)} \frac{1}{c_{i,r}} \boldsymbol{W}^{k}_r \boldsymbol{H}^{k-1}_j + \boldsymbol{W}^{k}_0 \boldsymbol{H}^{k-1}_i )$$

可以发现，RGCN和GCN很像，区别在于RGCN公式上简写了标准化的常数，令其为$c_{i,r}$，还增加了 $r$ 这个参数，用来表示不同的边，每个边对应着不同的可学习参数$\boldsymbol {W}_r$。下图也能说明这个公式，对于rel_1这个关系，有4个in的连接和2个out的连接，所以对应着左侧前两个框，通过不同的绿色框$\boldsymbol {W}_r$得到特征，对于其他关系也是这样。特别地，对于self-loop，也有一个特殊的绿框。之后，得到的特征相加在一起，再进行激活得到这个节点的输出。

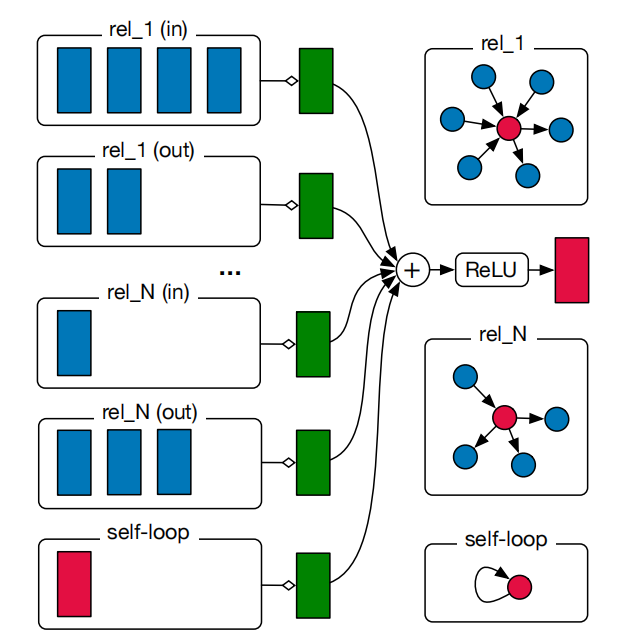
参考这篇知乎，RGCN还提出了正则化的问题，当网络中存在很多不同类型的边时，每个边对应的$\boldsymbol {W}_r$的数据量不同，可能有的边数量很少，所以会产生对于一些边的过拟合的情况。RGCN提出了basis decomposition和block diagonal decomposition两种正则化方法。

原本的$\boldsymbol {W}$应该是一个[num_types, in, out]的矩阵，使用第一种方式，就是拆成了[num_types, num_bases]和[num_bases, in, out]两个矩阵，这样就是通过学习压缩边的个数。

使用第二种方式，则是得到一个[num_types, num_bases * s_in * s_out]的矩阵，其中s_in=in/num_bases

这一块实在没看懂，假如有人看懂了希望能告诉我，下面是一些参考：

2107.10015.pdf (arxiv.org) 第五页

Intro to Relational - Graph Convolutional Networks - YouTube