计算机视觉学习笔记#3 拟合：最小二乘法、RANSAC、Hough霍夫变换（附代码）

计算机视觉学习笔记#3 拟合

之前提到的边缘检测虽然能得到线，但是无法得到线的位置，而在下图这种例子中，假如要检测硬币的位置，那需要知道画面中圆边缘和圆心的位置。拟合能够用数学来描述出结果，而不是像素。

拟合的难点

要找到车的拟合边缘有以下难点

• 那图中可能存在许多不属于这个车的边缘（噪声）
• 车可能被遮挡。
• 车包含多个线条，在提取一条线的时候，其他线都是噪声。

最小二乘法：所有点都是有效点的情况

注意最小二乘法的距离是数轴上的距离。如图先定义一个能量函数（类似机器学习的loss），然后把用矩阵表示方程，则$Y=XB$，然后我们希望能量函数$E=||Y-XB||^2$最小，就求导等于0时为极值。

**缺陷：**无法处理垂直线段的情况，因为此时这个距离未定义

全最小二乘法

距离的定义改成点到线段的举例，所以改了一下能量函数。

RANSAC：一条直线+多点噪声

RANSAC是RANdom SAmple Consensus的缩写，即基于随机采样的一种方式，是一种能够处理拟合有较多噪声的一条直线的方法。

核心思想是先选择两个点构成一条直线，然后其余点给这条直线进行投票。如图，第一步首先选择两个点，然后第二步构建一条直线，第三步计算其余点到直线的距离，第四步选择距离较小的点为这条线进行投票，第五步重复。

RANSAC也可以拟合其他情况，那么方法扩展为：

1. 选择目标模型的最少确定点（比如三角形就是三个点，圆形也是三个点，正方形是两个点）
2. 构建模型，并计算其余点对于这个模型的误差（比如距离圆的距离，距离正方形最近边的距离）
3. 设置阈值，误差小于阈值的点投上一票
4. 重复

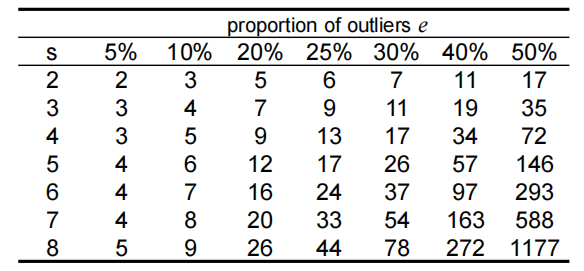
现在还有个问题，就是到底要重复多少次才能找到理想的线？假设总共循环$N$次，有比例$e$的噪声点，线的可信度为$p$，那么：

$$(1-(1-e)^2)^N = 1-p$$

左边选择两个属于直线的点的概率为$(1-e)^2$，其他情况则是1减去这个值，也就是错误情况。假如实验错误了$N$次，也就等于右式。经过计算可以得到下表

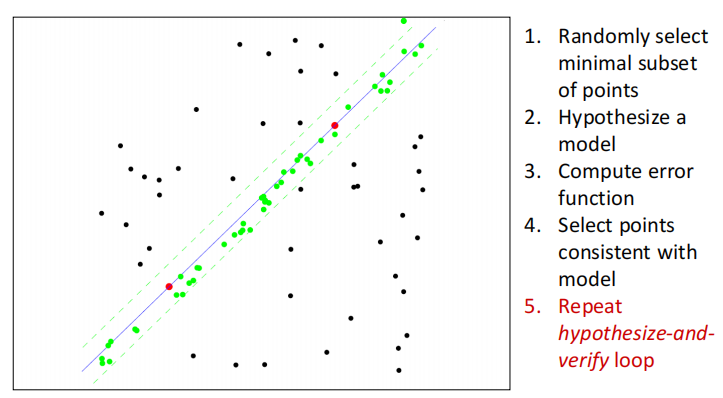
在确定最终结果的时候，我们记录了许多条线对应得到的投票数，假如设置一个投票阈值，也可以实现提取多条线。

Python实现 RANSAC算法检测直线、圆、正方形

代码有点长，不直接放在这里了，放Github上，注释很全，代码风格也还行hhh，效果如下：

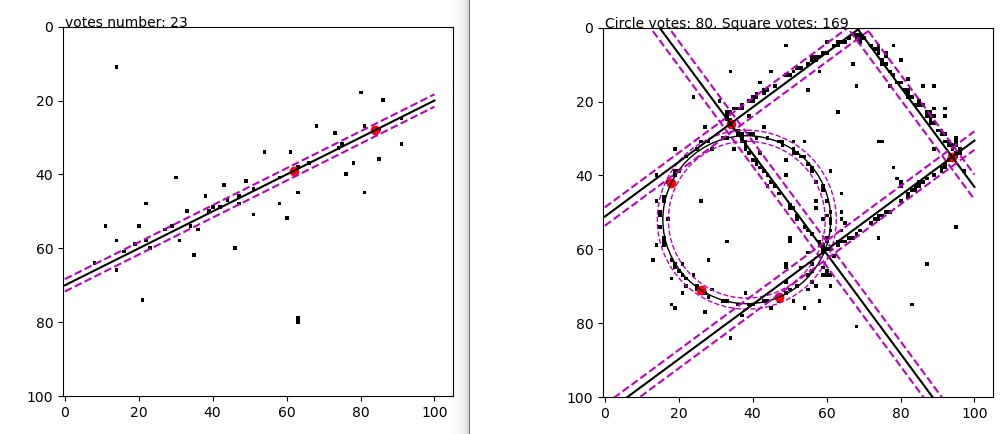
Hough 霍夫变换：多条直线

初步思想

主要思想是转换空间+投票。这种方法能够处理多条直线、高噪声甚至直线部分点缺失的情况。

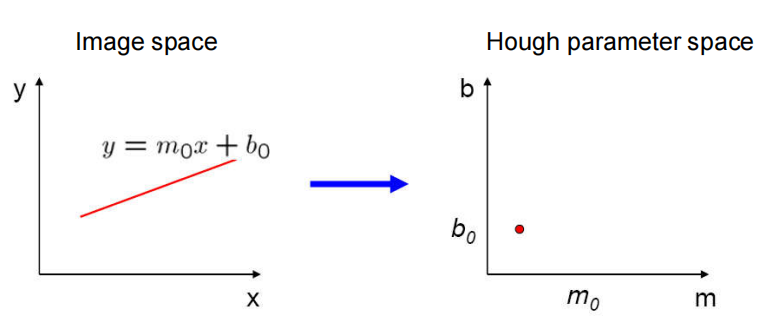
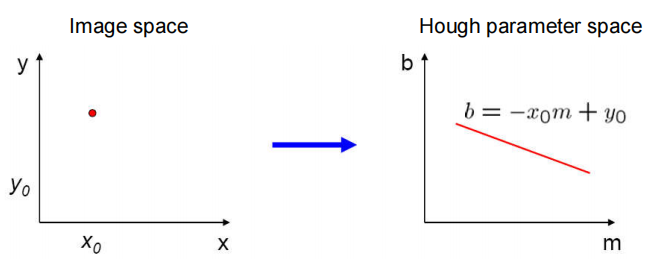
如图，霍夫变换能让图像空间的一条直线映射到霍夫空间的一个点（下图1），而图像空间的一个点映射到霍夫空间的一条线（下图2）。图像域的直线方程为$y=m_0x+b_0$，其中有两个确定直线的参数$m_0,b_0$，这两个参数能够构成霍夫参数空间，即以$m_0$为横坐标，$b_0$为纵坐标。

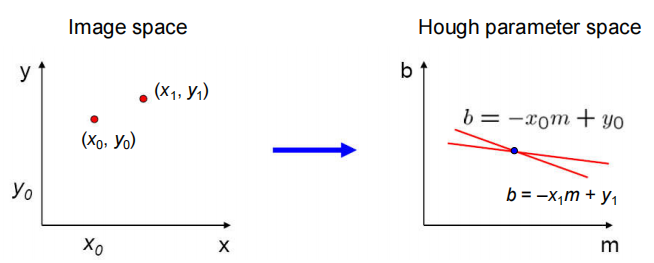
假如图像空间有许多个点，那在霍夫空间上就会有许多条直线（如下图3），这些直线会有一个交点，那这个霍夫空间的交点可以映射回一条直线。

另外，由于噪声等因素，在霍夫空间可能不会有明显的一个交点，所以会离散化霍夫空间，分成许多小格子，每条线会给经过的小格子投票，得到票数越多的小格子就越可能是交点的位置。

实际思想：极坐标

那么现在还有问题，假如图像空间有垂直线，那么$m$会趋近于无穷。这个的解决方法就是使用极坐标。如图，一条直线对应的$\theta,|\rho|$就是过原点的法线角度和长度。（此处图有点小错误，$\rho$可能是负数，距离应该取绝对值）。

• 图像空间的直线：$x\cos\theta_0+y\sin\theta_0=\rho_0$ -> $(\theta_0,\rho_o)$。
• 图像空间的点：$(x_0,y_0)$ -> $x_0\cos\theta+y_0\sin\theta=\rho$ 。

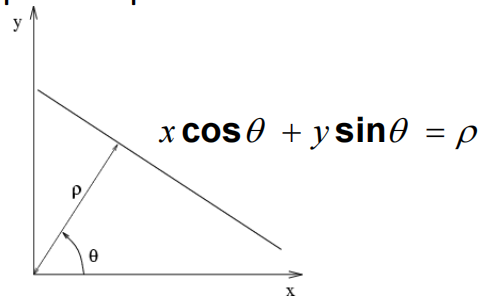
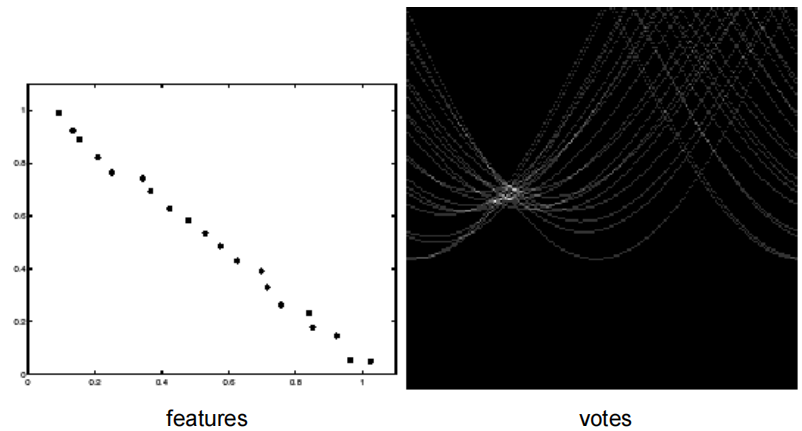
那么在极坐标进行投票就是对于所有$\theta\in[0,\pi]$，计算$\rho=x_0\cos\theta+y_0\sin\theta$，然后在对应的投票矩阵中+1。下面是一些例子：

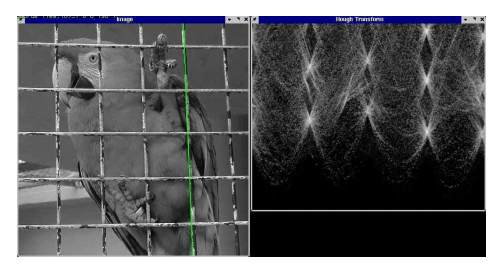
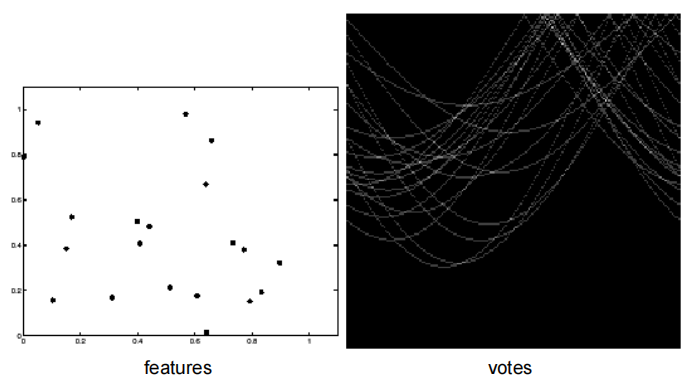
霍夫变换噪声分析

当噪声增加的时候，可能在霍夫空间较难找出一个点，而图像完全是噪声、没有直线的时候，在霍夫空间也可能有交点，从而识别出线。解决方法是相邻区间加权，就像高斯平滑相对平均平滑一样。

利用梯度

在边缘检测的时候，其实能够检测到一个点对应的直线方向，所以能得到一个具体的$\theta$，所以就不用对于所有$\theta\in[0,\pi]$了。

实践时也不是只用一个$\theta$，而是取一些区间

霍夫圆检测

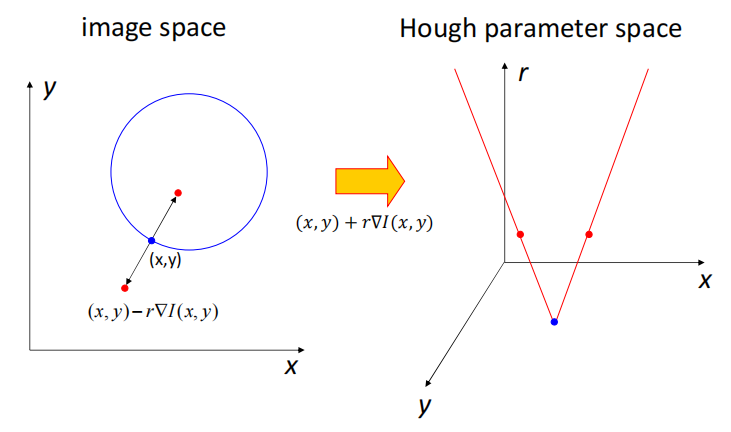
霍夫变换也能够用来检测圆，此时霍夫空间就是三维的了，对于图上的一个像素，它可能位于圆上，这个时候就是已知圆上一点，求圆心和半径。

通过边缘检测可以得到圆上一个点的梯度方向，易知圆心在梯度的正向或者反向上。所以霍夫空间上一个$r$就能有两个点（圆心）。这样就可以对于所有$r\in[0,图像边界]$进行投票。

霍夫变换直线检测代码

下面这份代码实现了使用极坐标霍夫变换检测直线，包括非最大化抑制、加权投票、检测多条直线等，注释超全。

代码也托管于Github

"""
coded by Kamino, kamino.plus@qq.com, 2022/4/15
未经许可不得转载
"""
import numpy as np
import cv2
import matplotlib.pyplot as plt
from tqdm import tqdm
from queue import PriorityQueue


def non_max_suppression(x):
    res = np.zeros_like(x)
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            if x[i, j] == 0:
                continue
            if np.sum(x[i - 1:i + 2, j - 1:j + 2] > x[i, j]) == 0:
                # print(x[i - 1:i + 2, j - 1:j + 2])
                res[i, j] = x[i, j]
    return res


def hough_line(x, theta_prec=1.0, rho_prec=2.0, topk=1, weight_mat: np.ndarray = None, non_max=False):
    if weight_mat is not None:  # 权重矩阵得是方阵，且边长要是单数
        assert len(weight_mat.shape) and weight_mat.shape[0] == weight_mat.shape[1] and weight_mat.shape[0] % 2 == 1
    # theta_ax和rho_ax是霍夫空间两个轴的量化数组
    # 使用theta_prec和rho_prec两个参数来确定量化精度，数字越大量化越粗
    theta_ax = np.deg2rad(np.arange(0, 180, theta_prec))
    max_rho = np.sqrt(x.shape[0] ** 2 + x.shape[1] ** 2)
    rho_ax = np.arange(-max_rho, max_rho, rho_prec)
    # 霍夫空间：是一个rho行theta列的空间
    hough_space = np.zeros((len(rho_ax), len(theta_ax)))
    for i in tqdm(range(x.shape[0])):  # i行 j列
        for j in range(x.shape[1]):
            # 找到二值图像中的1点
            if x[i, j] == 0:
                continue
            # 对于每一个theta的量化值求rho
            for t in range(len(theta_ax)):
                rh = j * np.cos(theta_ax[t]) + i * np.sin(theta_ax[t])
                # 量化得到的rho值，由于rho可能为负数，而数组是没有负数索引的
                # （虽然python的负索引有倒数的意义），所以我们要平移到正确的
                # 位置上。
                # 1.加轴的最大值 2.除以精度 3.找到最近整数位
                # *4.给相邻区块加权添加
                # *5.非最大化抑制
                if weight_mat is None:
                    hough_space[int(round((rh + max_rho) / rho_prec)), t] += 1
                else:
                    tgt_point = (int(round((rh + max_rho) / rho_prec)), t)
                    offset = (weight_mat.shape[0] - 1) // 2
                    hot_area = hough_space[tgt_point[0] - offset:tgt_point[0] + offset + 1,
                               tgt_point[1] - offset:tgt_point[1] + offset + 1]
                    if hot_area.shape == weight_mat.shape:
                        hough_space[tgt_point[0] - offset:tgt_point[0] + offset + 1,
                        tgt_point[1] - offset:tgt_point[1] + offset + 1] += weight_mat
    if non_max is True:
        hough_space = non_max_suppression(hough_space)

    # 用优先队列（大顶堆）找到前n个结果
    if topk == 1:
        points = np.where(hough_space == np.max(hough_space))
        return (rho_ax[points[0]], theta_ax[points[1]]), hough_space
    else:
        queue = PriorityQueue()
        for i in range(hough_space.shape[0]):
            for j in range(hough_space.shape[1]):
                queue.put((-hough_space[i, j], rho_ax[i], theta_ax[j], i, j))
        res = [queue.get()[1:] for _ in range(topk)]
        return res, hough_space


img = cv2.imread("ironnet_small.jpg", cv2.IMREAD_GRAYSCALE)
canny_img = cv2.Canny(img, 200, 230)
kernel = np.array([[2, 4, 5, 4, 2], [4, 9, 12, 9, 4], [5, 12, 15, 12, 5], [4, 9, 12, 9, 4], [2, 4, 5, 4, 2]]) / 159
rho_thetas, hough_img = hough_line(canny_img, topk=10, rho_prec=1, theta_prec=0.5, weight_mat=None, non_max=True)

# 下面都是绘图了
# figure1是对比
fig = plt.figure(1)
ax = plt.subplot(2, 1, 1)
ax.imshow(img, cmap=plt.get_cmap('gray'))
ax.set_title('Result')
print("*" * 30)
print("预测出的直线方程")
for rho, theta, _, _ in rho_thetas:
    print(f"x*{round(np.cos(theta), 2)}+y*{round(np.sin(theta), 2)}={round(rho / 2, 2)}")
    x_ = np.arange(0, canny_img.shape[1])
    y_ = (rho - x_ * np.cos(theta)) / np.sin(theta)
    ax.plot(x_, y_, 'red')
plt.ylim([img.shape[0], 0])
print("*" * 30)
ax = plt.subplot(2, 1, 2)
ax.imshow(canny_img, cmap=plt.get_cmap('gray'))
ax.set_title('Canny')
# figure2是霍夫空间可视化
fig = plt.figure(2)
ax = plt.subplot(1, 1, 1)
ax.imshow(hough_img, origin='lower')
for _, _, ri, ti in rho_thetas:
    ax.scatter(ti, ri)
ax.set_ylabel(r'$\rho$')
ax.set_xlabel(r'$\theta$')
ax.set_title('Hough space')
plt.show()