背包密码学
本文最后更新于:2022年7月21日 下午
背包密码学
参考文献:
Knapsack Encryption Algorithm in Cryptography - GeeksforGeeks
密码学——公钥密码体系之背包算法1 - 哔哩哔哩 (bilibili.com)
谁能用通俗语言解释一下NP完全问题? - 知乎 (zhihu.com)
假如不太懂模运算可以参考我的另外一篇博客RSA加密算法 - Kamino’s Blog
在密码学领域,于1978年由Ralph Merkle 和Mertin Hellman发明的**背包加密算法(Knapsack Encryption Algorithm)**是第一个通用的公钥加密算法。这个算法基于一个NP完全问题——背包问题,虽然后面发现这个算法并不安全,但是仍然值得我们学习。
先科普一下什么是NP完全问题:
P问题是一类可以在多项式时间内求解的问题,NP问题是一类可以在多项式时间内验证解是否正确的问题。
显然,但是目前人们想知道的是
NP-C或NP完全问题指的是“多项式复杂程度的非确定性问题”,所有的NP问题都可以约化到NP-C问题(即可以用NP-C问题的解法来解决NP问题,但NP-C问题的解法可能时间复杂度更高)。
背包问题指的是:给定一批不同体积的物品和一个背包容积,能够将物品中的几件放进这个背包,使背包刚好装满。
一般来说,解这个问题所需要的时间随着物品个数的增加呈指数增长,但其中包含一类可以在线性时间内可解的问题,背包算法的思想就是将明文看作背包问题的解,明文长度等于物品个数,而密文就是物品体积和。
| 明文 | 1 | 0 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|
| 背包/秘钥 | 1 | 4 | 7 | 10 | 17 | 20 |
| 密文 | 1+ | 0+ | 7+ | 10+ | 0+ | 20=38 |
容易解决的背包问题就是使用超递增序列,这种序列的每一项都大于它之前所有项之和,即。比如上面的1 4 7 10 17 20就不是,而2 3 6 13 27 52就是。使用这种序列的话,只需要逐渐取最大的物品放进背包即可。例如总容量70的背包,则先放52,然后发现27放不了,就放13,然后发现6放不了,就放3,最后放2。
下面介绍背包加密算法的具体流程:
- 取一个递增序列作为私钥:(
2 3 6 13 27 52) - 取一个与序列中所有数互质的整数,再取一个大于所有数的整数()
- 计算,得到一个新序列作为公钥(
62 93 81 88 102 37) - 背包长度为6,所以二进制明文按照6bit分组,1表示存在,0表示不存在,然后计算总体积(明文
101101,则公钥加密密文为268) - 计算n的乘法逆元。()
- 计算,然后解背包问题得到明文。(
73=52+13+6+2(101101))
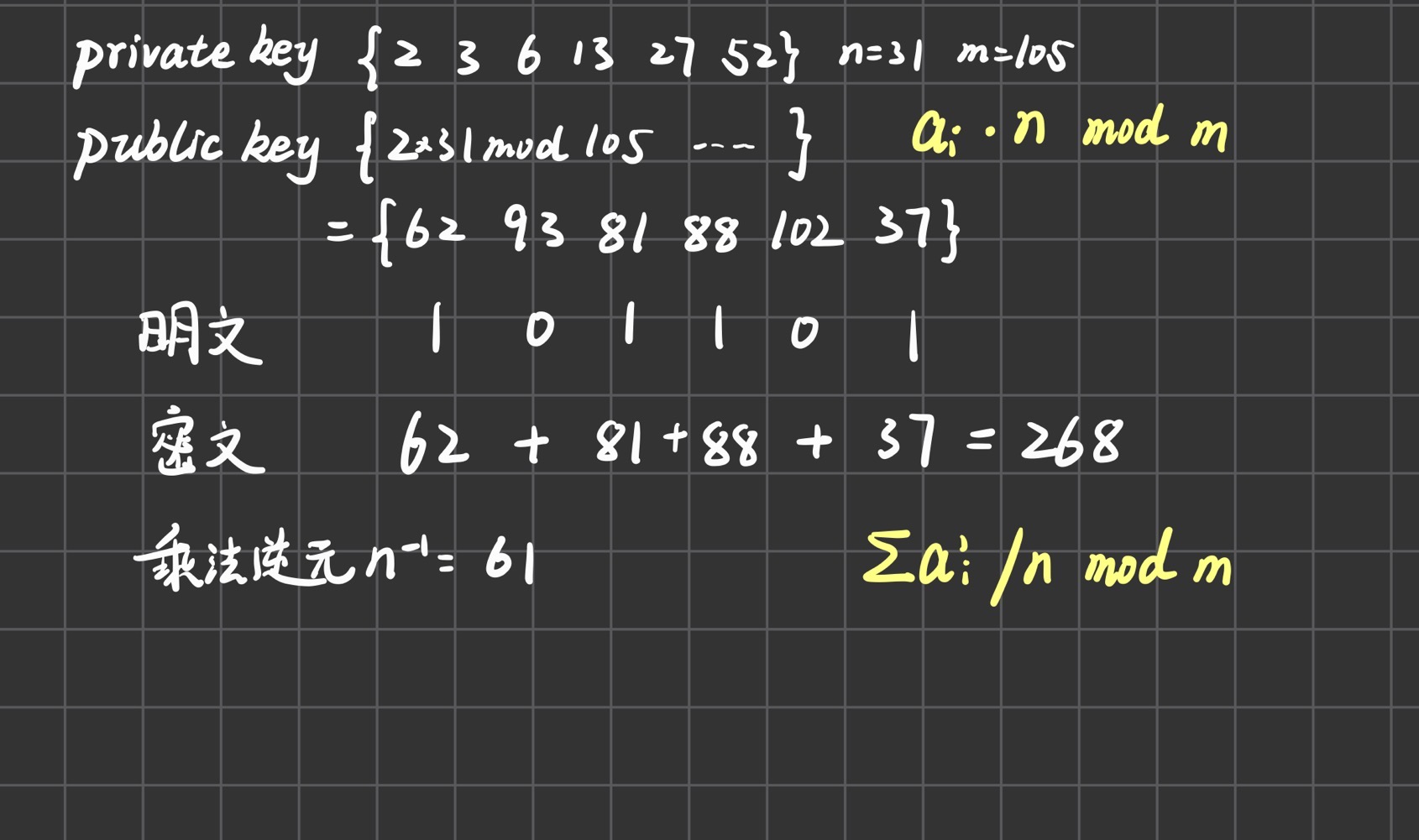
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!