我的机器学习课笔记 #4-SVM支持向量机

[TOC]

SVM，全称Support Vector Machine，即支持向量机，是一种监督学习算法，基础的SVM是二分类线性模型，但可通过核函数拓展至非线性分类或者用其他方法拓展至多分类模型。本文是学习SVM基础模型、软间隔与正则项、核函数以及数学上的求解方法时所做的笔记。

SVM基础模型

SVM算法的动机就是想画一条线，能最好地分开训练样本中的两个类别。如何判断“最好”呢？判断离这条线最近的几个点与线的距离，这个距离越大，效果就越好。判断距离时选中的那几个点被叫做支持向量，SVM的训练结果直接由这几个支持向量决定，这叫做SVM的稀疏性。

理论求解

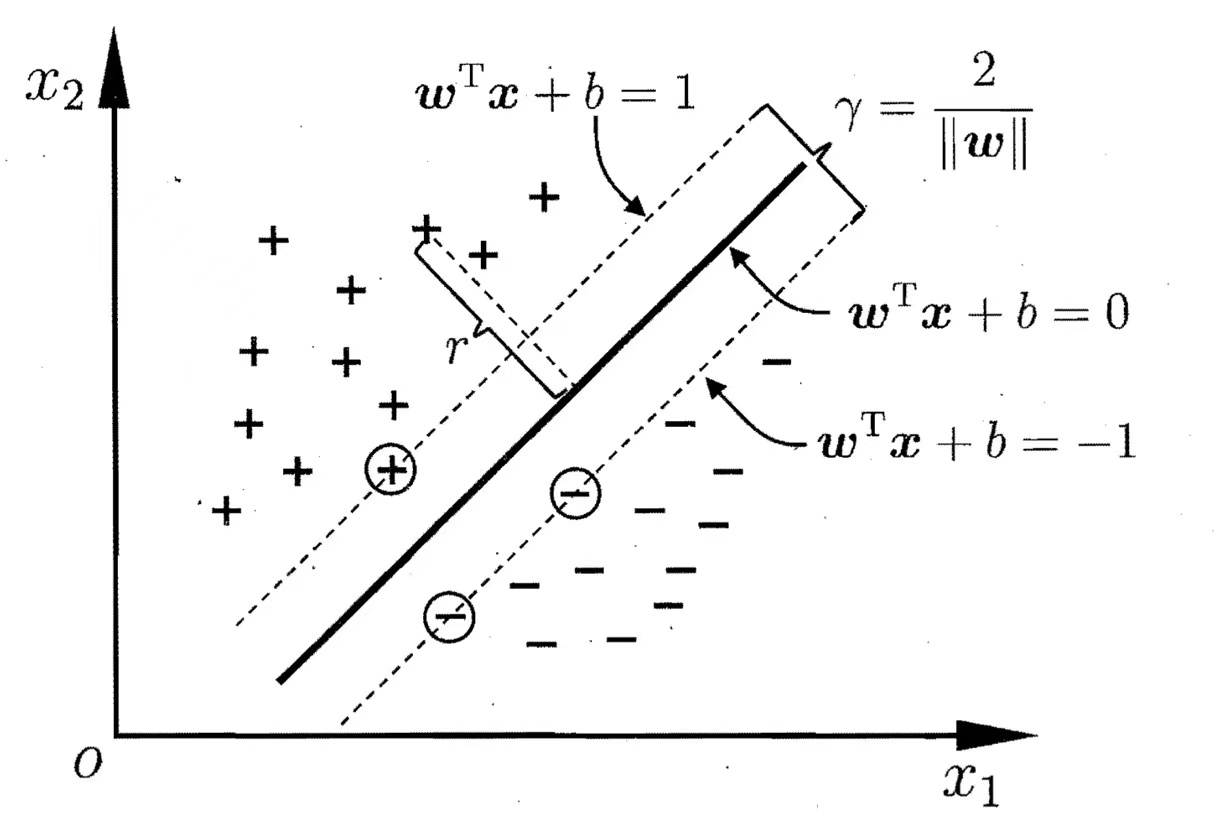
要画的那一条“线”其实是一个超平面，数学上用 $\boldsymbol{w^Tx}+b=0$这个方程表示*（几何中一条线的方程是Ax+By+C=0，一个面的方程是Ax+By+Cz+D=0，以此类推到多维空间的超平面数学方程）*

而点到超平面的距离公式是$ d=\frac{|\boldsymbol{w^Tx}+b|}{||w||}$（几何中一个三维空间的点到平面距离公式是 $d=\frac{|Ax+By+Cz+D|}{\sqrt{A^2+B^2+C^2}}$，以此类推）

此时新假设两个平行于$\boldsymbol{w^Tx}+b=0$的超平面，一个是$\boldsymbol{w^Tx}+b=1$，另一个是$\boldsymbol{w^Tx}+b=-1$，需要找到的 $\boldsymbol{w^T}$需要满足以下条件，而通过平面间距的公式得到新假设的这两个超平面间隔为 $\gamma=\frac{2}{||w||}$。

所以我们需要优化的问题是：

$$argmin_{w,b}(\frac{||w||}{2}) \quad s.t. y_i(\boldsymbol{w^Tx_i}+b) \ge 1$$

利用对偶问题求解（参考西瓜书附录）

拉格朗日乘子法的解释：拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子，可将有d个变量、k个约束的最优化问题转换为d+k个变量、无约束的最优化问题。

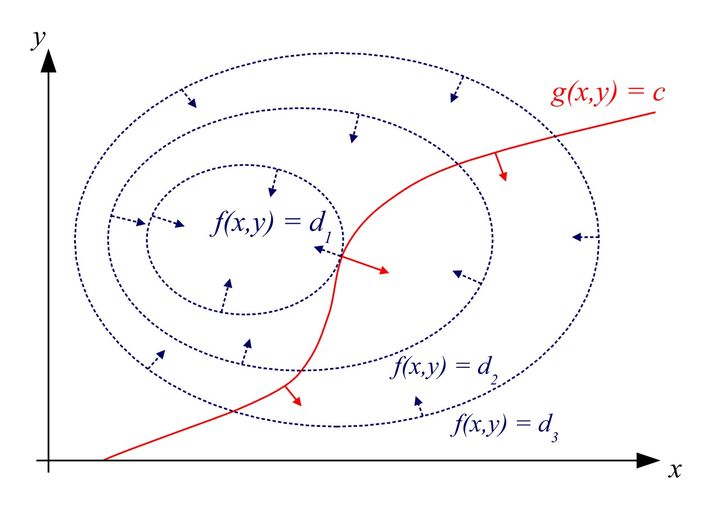
如图，假如函数是 $f(x,y)$，约束是 $g(x,y)=C$，那么在最优点（图中等高线交点）函数梯度和约束梯度方向相同或相反，即 $\nabla f(x_i,y_i) + \lambda \nabla g(x_i,y_i) = 0$。此时定义另一个函数 $L(x,y,\lambda)=f(x,y)+\lambda g(x,y)$，则 $\frac{\partial L}{\partial x,y} = \nabla f(x_i,y_i) + \lambda \nabla g(x_i,y_i)$。所以原问题就转换成了最后这个方程的最优化问题。

假如约束不是个等式，而是不等式，也可以使用这种方法。假设函数是 $f(x,y)$，约束是 $g(x,y) \le 0$。假如最优点$(x_i,y_i)$满足$g(x_i,y_i)<0$，那约束就不起作用，直接对原始做无约束最优化；假如最优点$(x_i,y_i)$满足$g(x_i,y_i)=0$，那就和等式约束的情况一样了，但是此时函数梯度和约束梯度方向必然相反，所以此时 $\lambda>0$。结合两种情况，归纳成KKT条件：

$$g(x,y) \le 0 \quad \lambda \ge 0 \quad \lambda g(x)=0$$

使用拉格朗日乘子法求SVM的最优化问题：

将$argmin_{w,b}(\frac{||w||}{2}) \quad s.t. y_i(\boldsymbol{w^Tx_i}+b) \ge 1$转换成拉格朗日函数即

$$L(\boldsymbol w, b, \boldsymbol \alpha)= \frac{||w||^2}{2} + \sum^m_{i=1} \alpha_i (1-y_i(\boldsymbol{w^Tx_i}+b))$$

满足KKT条件：

$$1-y_i(\boldsymbol{w^Tx_i}+b) \le 0 \quad \alpha_i \ge 0 \quad \alpha_i (1-y_i(\boldsymbol{w^Tx_i}+b))=0$$

现在问题就只剩下解出$L(\boldsymbol \alpha)$的最大值（此处留坑）

核函数

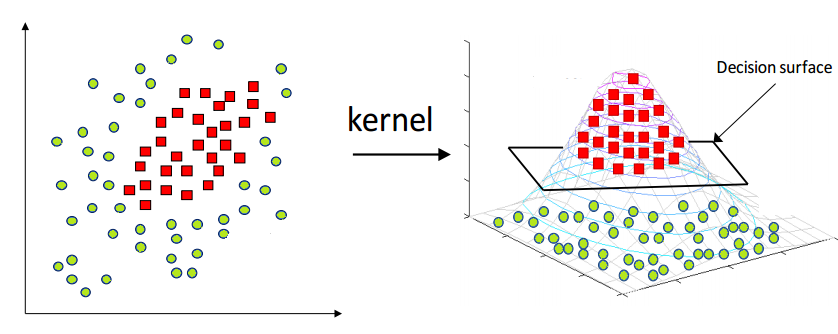
核函数，或者叫做核技巧，是在SVM中用来将线性拓展到非线性的工具。对于图中左边这种无法用一根直线划分的数据分布，使用某种映射函数 $\phi(x)$映射到高维空间后，就能用一个平面划分。但是$\phi(x)$ 有很多种，而且映射之后也无法保证是线性可分的。只能保证假如原始空间是有限维度的，那么一定会有一个高维特征空间使样本线性可分。

在使用映射函数提升维度后，对偶问题变成了 $最大化 -\frac{1}{2}\sum^m_{i=1}\sum^m_{j=1} \alpha_i \alpha_j y_i y_j \phi(\boldsymbol{x_i})^T\phi(\boldsymbol{x_j}) + \sum^m_{i=1}\alpha_i$，但是求 $\phi(\boldsymbol{x_i})^T\phi(\boldsymbol{x_j})$是在是太麻烦了，需要升维之后再求内积，所以我们使用核技巧，用核函数代替内积，即 $k(\boldsymbol{x_i, x_j}) = \phi(\boldsymbol{x_i})^T\phi(\boldsymbol{x_j})$。从这个角度来看，核函数就是计算样本映射到高维空间的内积。

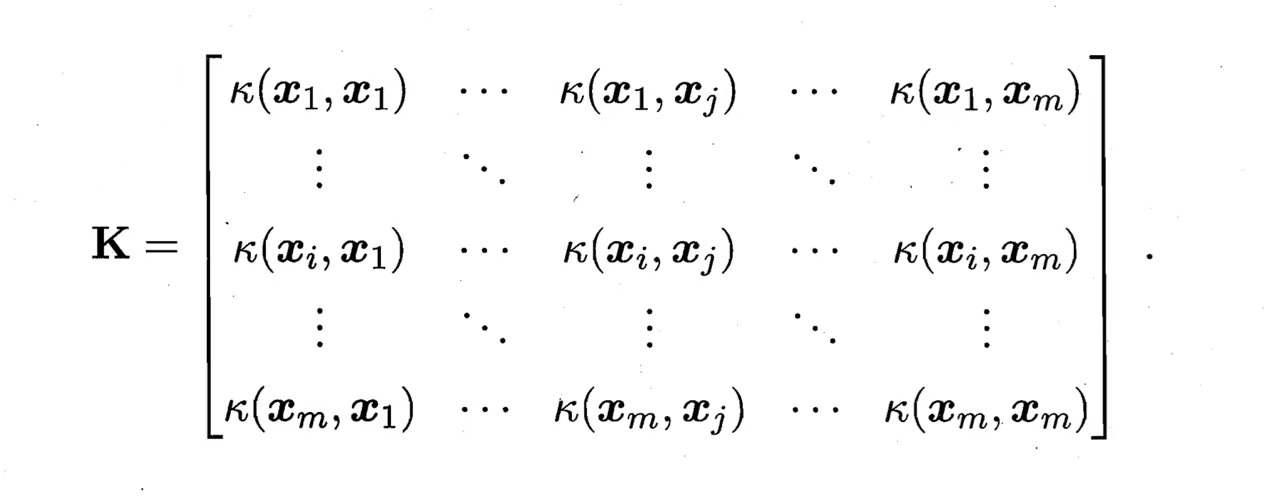
核函数对应着一个核矩阵，对于任意对称函数，只要这个矩阵是半正定的，那这个函数就能当做核函数，一个半正定矩阵就暗中对应着一个高维空间。

对于这个核函数的选择，西瓜书上列了这些。

对称函数：$f(x, y) = f(y,x)$

半正定矩阵：给定一个$n\times n$的实数对称矩阵$A$，若对于任意长度$n$的向量$\boldsymbol{x}$，有$\boldsymbol{x^TAx} \ge 0$恒成立，则为半正定矩阵。$y=\boldsymbol{x^TAx}$就和$y=ax^2$差不多，要它$\ge 0$恒成立，就是要$A$满足一个从另一个角度$\ge 0$的条件。

证明：$K(x^{(i)},x^{(j)})$是$K$矩阵$i$行$j$列的值，又可以看作是某两个向量特征映射之后的内积，对于高维向量的单独一个值，就是向量通过$\phi_k$函数（k是高维的维度）的出来的单个值。

软间隔

前面提到就算用了核函数也不能保证数据在高维空间是线性可分的，于是我们可以考虑保留少部分点是错误分类的。

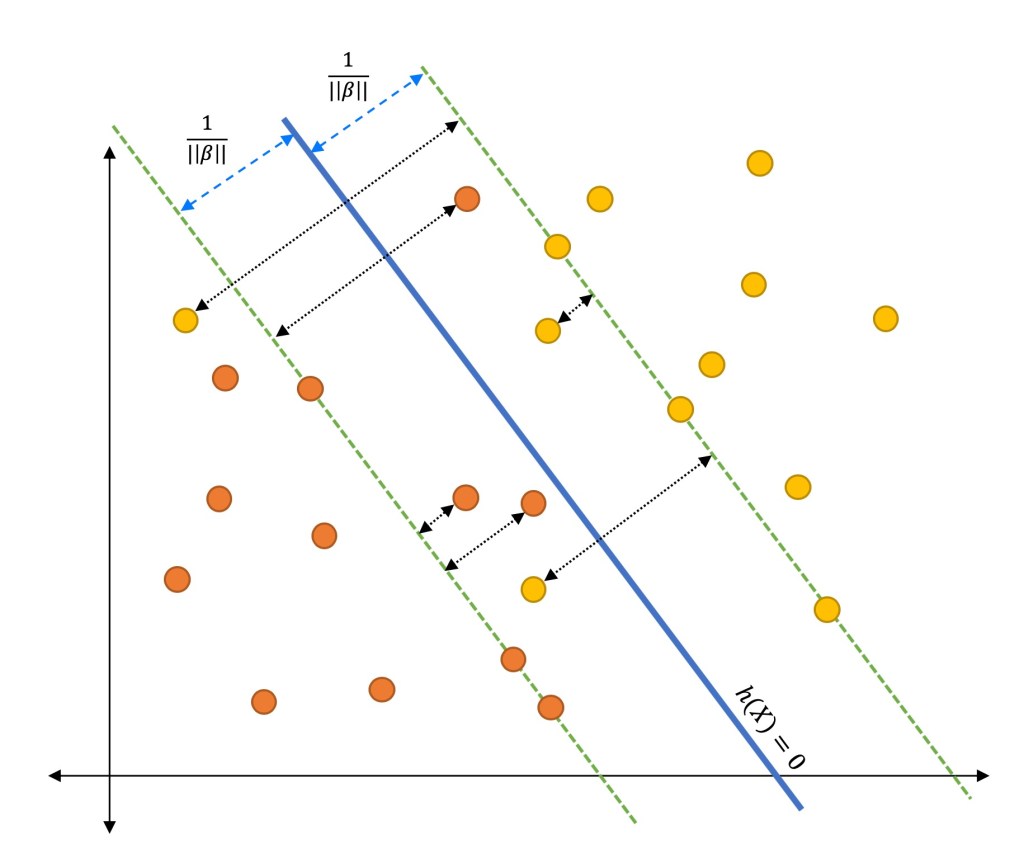
此时需要优化的问题变成了

$$argmin_{w,b}(\frac{||w||}{2} + C\sum^m_{i=1}\ell_{0/1}(y_i(\boldsymbol{w^Tx_i}+b) - 1))$$

其中$\ell_{0/1}(z)$是当$z<0$时为1，$z\ge0$时为0的函数。

$y_i(\boldsymbol{w^Tx_i}+b) < 1$时，点不位于超平面正确的那一侧，此时$\ell_{0/1}(z)=1$，第二项开始起作用，而作用就是作为一个正数，让loss的值变大，从而让优化算法使不符合要求的点尽量少。

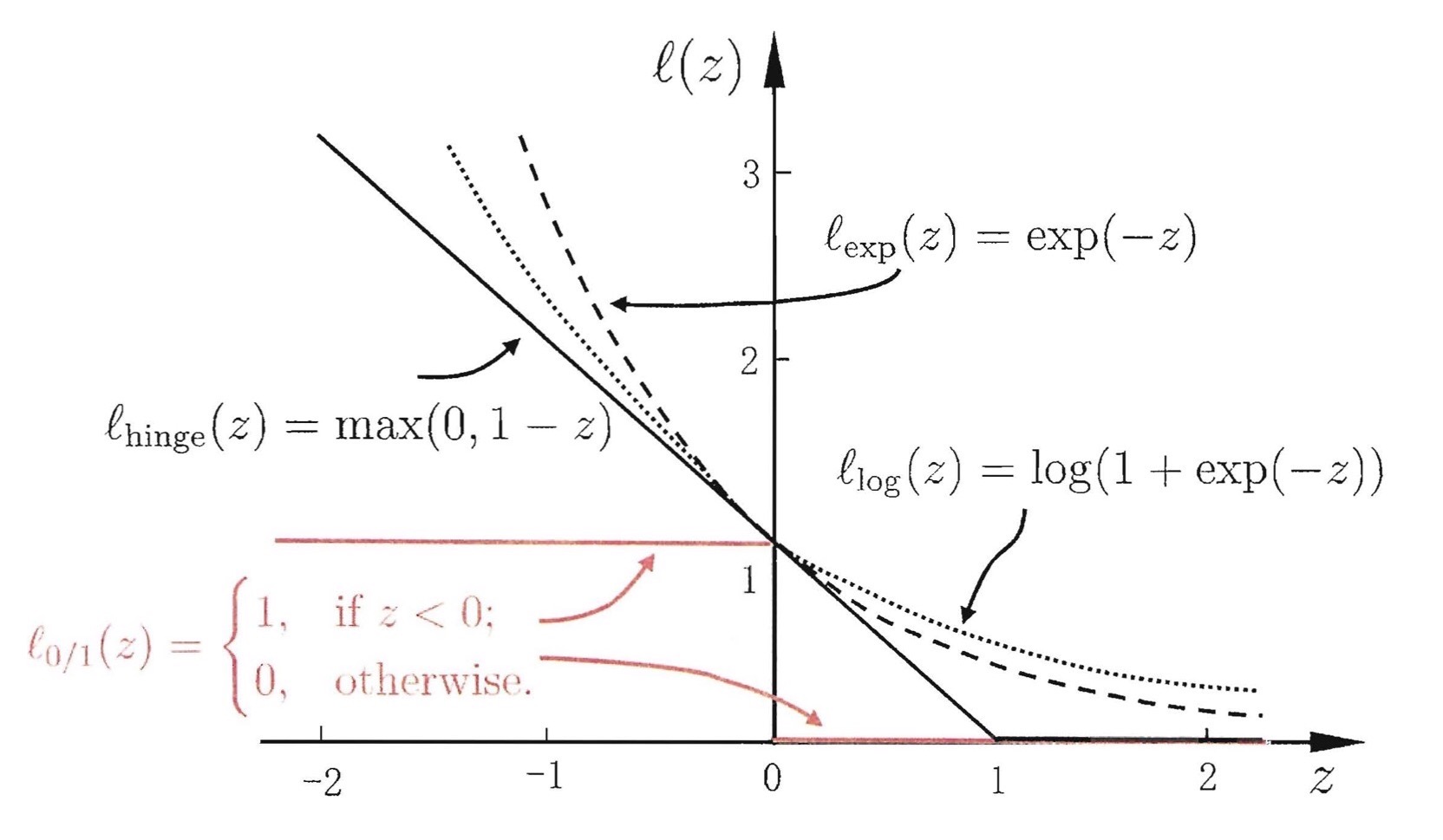
说到优化算法，上面说的$\ell_{0/1}(z)$明显是没有导数还不连续的，所以一般使用别的函数来替代它。如下图，有三种损失，分别是hinge损失、指数损失和对率损失，其中hinge损失用的最多。

下图$z<0$时即点在超平面（上图虚线）的另一侧，此时$\ell(z) \ge 1$；下图$0<z$时即点在超平面（上图虚线）的正确侧，但会根据点与分割线的距离给予不同的损失，此时$0 \le \ell(z) \le 1$。这样的话两个额外的超平面（上图虚线）就不是强行划分的界限了，而是形成了和距离有关的软间隔。

正则化

定义$\xi = \ell(y_i(\boldsymbol{w^Tx_i}+b) - 1)$，要优化的那一部分可以简写成下面这样：

$$argmin_{w,b}(\frac{||w||^2}{2} + C\sum^m_{i=1} \xi_i)$$

我们换个形式，也可以是这样：

$$argmin_{w,b}(\sum^m_{i=1} \xi_i + \lambda ||w||^2)$$

这样的话就很像逻辑回归添加了L2正则化的损失函数：$argmin_{w,b}(\sum^m_{i=1} (y-\hat{y})^2 + \lambda ||w||^2)$。两者的第一项被叫做经验风险，指模型在训练集学习到的经验；第二项被叫做结构风险，描述模型的某些性质，这一项又可以被叫做正则化项，而$\lambda$叫做正则化常数，用来获取结构上复杂度较小的模型。

参考文献

如何理解拉格朗日乘子法？ - 知乎 (zhihu.com)

Kernel Trick in SVM. Kernel Trick can solve this issue using… | by Siddhartha Sharma | Analytics Vidhya | Medium

浅谈「正定矩阵」和「半正定矩阵」 - 知乎 (zhihu.com)

SVM的核函数中为什么要求核矩阵是半正定的？ - 知乎 (zhihu.com)

Support Vector Machines for Beginners - Linear SVM - A Developer Diary